Sculpting Molecules in 3D: A Flexible Substructure Aware Framework for Text-Oriented Molecular Optimization

The integration of deep learning, particularly AI-Generated Content, with high-quality data derived from ab initio calculations has emerged as a promising avenue for transforming the landscape of scientific research. However, the challenge of designing molecular drugs or materials that incorporate multi-modality prior knowledge remains a critical and complex undertaking. Specifically, achieving a practical molecular design necessitates not only meeting the diversity requirements but also addressing structural and textural constraints with various symmetries outlined by domain experts. In this article, we present an innovative approach to tackle this inverse design problem by formulating it as a multi-modality guidance generation/optimization task. Our proposed solution involves a textural-structure alignment symmetric diffusion framework for the implementation of molecular generation/optimization tasks, namely 3DToMolo. 3DToMolo aims to harmonize diverse modalities, aligning them seamlessly to produce molecular structures adhere to specified symmetric structural and textural constraints by experts in the field. Experimental trials across three guidance generation settings have shown a superior hit generation performance compared to state-of-the-art methodologies. Moreover, 3DToMolo demonstrates the capability to generate novel molecules, incorporating specified target substructures, without the need for prior knowledge. This work not only holds general significance for the advancement of deep learning methodologies but also paves the way for a transformative shift in molecular design strategies. 3DToMolo creates opportunities for a more nuanced and effective exploration of the vast chemical space, opening new frontiers in the development of molecular entities with tailored properties and functionalities.

Companion Surface of Danger Cylinder and its Role in Solution Variation of P3P Problem

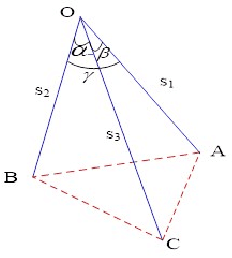
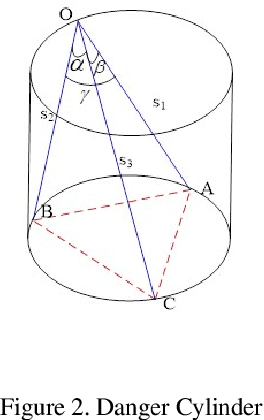
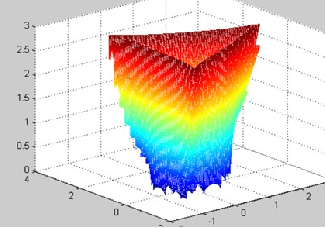
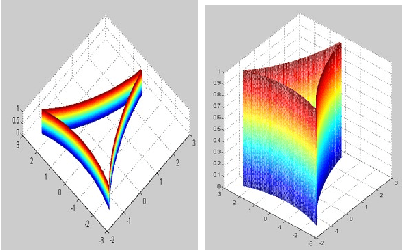
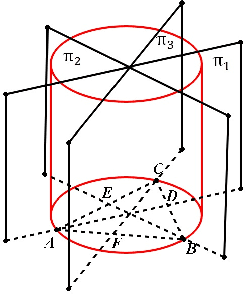
Traditionally the danger cylinder is intimately related to the solution stability in P3P problem. In this work, we show that the danger cylinder is also closely related to the multiple-solution phenomenon. More specifically, we show when the optical center lies on the danger cylinder, of the 3 possible P3P solutions, i.e., one double solution, and two other solutions, the optical center of the double solution still lies on the danger cylinder, but the optical centers of the other two solutions no longer lie on the danger cylinder. And when the optical center moves on the danger cylinder, accordingly the optical centers of the two other solutions of the corresponding P3P problem form a new surface, characterized by a polynomial equation of degree 12 in the optical center coordinates, called the Companion Surface of Danger Cylinder (CSDC). That means the danger cylinder always has a companion surface. For the significance of CSDC, we show that when the optical center passes through the CSDC, the number of solutions of P3P problem must change by 2. That means CSDC acts as a delimitating surface of the P3P solution space. These new findings shed some new lights on the P3P multi-solution phenomenon, an important issue in PnP study.

Geometric Interpretation of side-sharing and point-sharing solutions in the P3P Problem

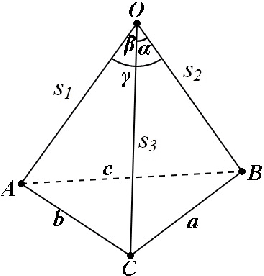
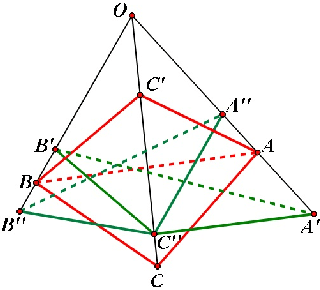
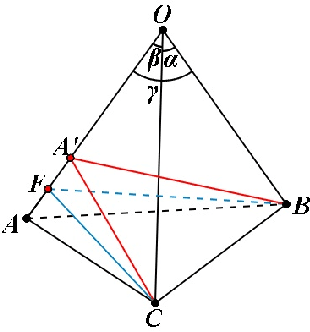
It is well known that the P3P problem could have 1, 2, 3 and at most 4 positive solutions under different configurations among its 3 control points and the position of the optical center. Since in any real applications, the knowledge on the exact number of possible solutions is a prerequisite for selecting the right one among all the possible solutions, the study on the phenomenon of multiple solutions in the P3P problem has been an active topic . In this work, we provide some new geometric interpretations on the multi-solution phenomenon in the P3P problem, our main results include: (1): The necessary and sufficient condition for the P3P problem to have a pair of side-sharing solutions is the two optical centers of the solutions both lie on one of the 3 vertical planes to the base plane of control points; (2): The necessary and sufficient condition for the P3P problem to have a pair of point-sharing solutions is the two optical centers of the solutions both lie on one of the 3 so-called skewed danger cylinders;(3): If the P3P problem has other solutions in addition to a pair of side-sharing ( point-sharing) solutions, these remaining solutions must be a point-sharing ( side-sharing ) pair. In a sense, the side-sharing pair and the point-sharing pair are companion pairs. In sum, our results provide some new insights into the nature of the multi-solution phenomenon in the P3P problem, in addition to their academic value, they could also be used as some theoretical guidance for practitioners in real applications to avoid occurrence of multiple solutions by properly arranging the control points.