Geometric Interpretation of side-sharing and point-sharing solutions in the P3P Problem

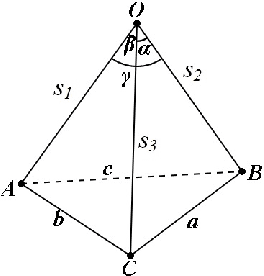
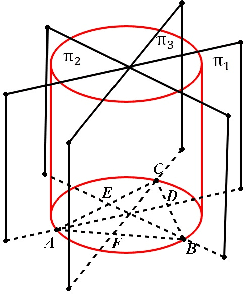
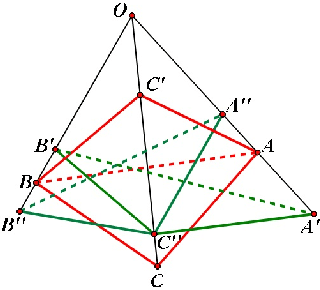
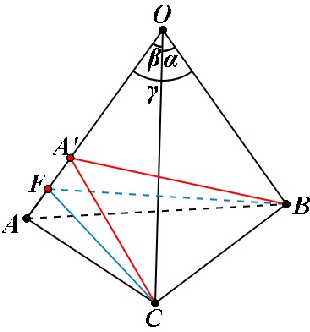
It is well known that the P3P problem could have 1, 2, 3 and at most 4 positive solutions under different configurations among its 3 control points and the position of the optical center. Since in any real applications, the knowledge on the exact number of possible solutions is a prerequisite for selecting the right one among all the possible solutions, the study on the phenomenon of multiple solutions in the P3P problem has been an active topic . In this work, we provide some new geometric interpretations on the multi-solution phenomenon in the P3P problem, our main results include: (1): The necessary and sufficient condition for the P3P problem to have a pair of side-sharing solutions is the two optical centers of the solutions both lie on one of the 3 vertical planes to the base plane of control points; (2): The necessary and sufficient condition for the P3P problem to have a pair of point-sharing solutions is the two optical centers of the solutions both lie on one of the 3 so-called skewed danger cylinders;(3): If the P3P problem has other solutions in addition to a pair of side-sharing ( point-sharing) solutions, these remaining solutions must be a point-sharing ( side-sharing ) pair. In a sense, the side-sharing pair and the point-sharing pair are companion pairs. In sum, our results provide some new insights into the nature of the multi-solution phenomenon in the P3P problem, in addition to their academic value, they could also be used as some theoretical guidance for practitioners in real applications to avoid occurrence of multiple solutions by properly arranging the control points.