Companion Surface of Danger Cylinder and its Role in Solution Variation of P3P Problem

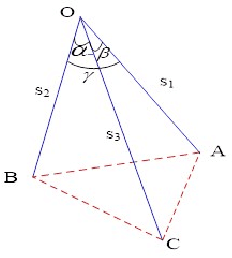
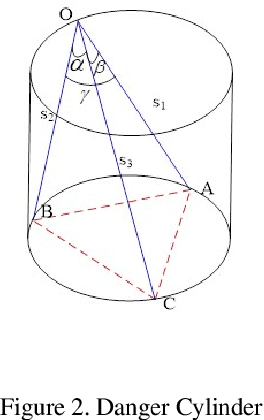
Traditionally the danger cylinder is intimately related to the solution stability in P3P problem. In this work, we show that the danger cylinder is also closely related to the multiple-solution phenomenon. More specifically, we show when the optical center lies on the danger cylinder, of the 3 possible P3P solutions, i.e., one double solution, and two other solutions, the optical center of the double solution still lies on the danger cylinder, but the optical centers of the other two solutions no longer lie on the danger cylinder. And when the optical center moves on the danger cylinder, accordingly the optical centers of the two other solutions of the corresponding P3P problem form a new surface, characterized by a polynomial equation of degree 12 in the optical center coordinates, called the Companion Surface of Danger Cylinder (CSDC). That means the danger cylinder always has a companion surface. For the significance of CSDC, we show that when the optical center passes through the CSDC, the number of solutions of P3P problem must change by 2. That means CSDC acts as a delimitating surface of the P3P solution space. These new findings shed some new lights on the P3P multi-solution phenomenon, an important issue in PnP study.

New insights on Multi-Solution Distribution of the P3P Problem

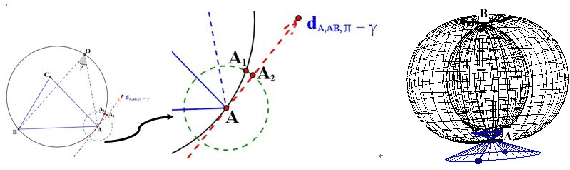
Traditionally, the P3P problem is solved by firstly transforming its 3 quadratic equations into a quartic one, then by locating the roots of the resulting quartic equation and verifying whether a root does really correspond to a true solution of the P3P problem itself. However, a root of the quartic equation does not always correspond to a solution of the P3P problem. In this work, we show that when the optical center is outside of all the 6 toroids defined by the control point triangle, each positive root of the Grunert's quartic equation must correspond to a true solution of the P3P problem, and the corresponding P3P problem cannot have a unique solution, it must have either 2 positive solutions or 4 positive solutions. In addition, we show that when the optical center passes through any one of the 3 toroids among these 6 toroids ( except possibly for two concentric circles) , the number of the solutions of the corresponding P3P problem always changes by 1, either increased by 1 or decreased by 1.Furthermore we show that such changed solutions always locate in a small neighborhood of control points, hence the 3 toroids are critical surfaces of the P3P problem and the 3 control points are 3 singular points of solutions. A notable example is that when the optical center passes through the outer surface of the union of the 6 toroids from the outside to inside, the number of the solutions must always decrease by 1. Our results are the first to give an explicit and geometrically intuitive relationship between the P3P solutions and the roots of its quartic equation. It could act as some theoretical guidance for P3P practitioners to properly arrange their control points to avoid undesirable solutions.

Geometric Interpretation of side-sharing and point-sharing solutions in the P3P Problem

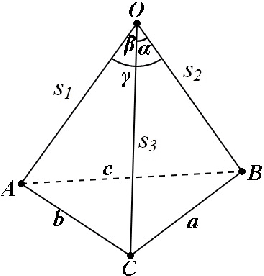
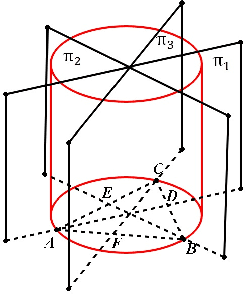
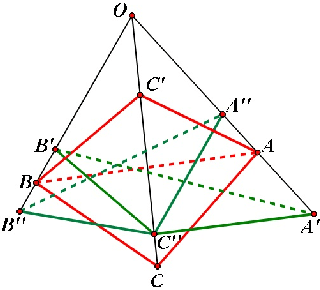
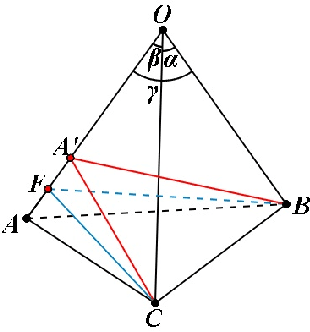
It is well known that the P3P problem could have 1, 2, 3 and at most 4 positive solutions under different configurations among its 3 control points and the position of the optical center. Since in any real applications, the knowledge on the exact number of possible solutions is a prerequisite for selecting the right one among all the possible solutions, the study on the phenomenon of multiple solutions in the P3P problem has been an active topic . In this work, we provide some new geometric interpretations on the multi-solution phenomenon in the P3P problem, our main results include: (1): The necessary and sufficient condition for the P3P problem to have a pair of side-sharing solutions is the two optical centers of the solutions both lie on one of the 3 vertical planes to the base plane of control points; (2): The necessary and sufficient condition for the P3P problem to have a pair of point-sharing solutions is the two optical centers of the solutions both lie on one of the 3 so-called skewed danger cylinders;(3): If the P3P problem has other solutions in addition to a pair of side-sharing ( point-sharing) solutions, these remaining solutions must be a point-sharing ( side-sharing ) pair. In a sense, the side-sharing pair and the point-sharing pair are companion pairs. In sum, our results provide some new insights into the nature of the multi-solution phenomenon in the P3P problem, in addition to their academic value, they could also be used as some theoretical guidance for practitioners in real applications to avoid occurrence of multiple solutions by properly arranging the control points.