Companion Surface of Danger Cylinder and its Role in Solution Variation of P3P Problem
Paper and Code
Jun 04, 2019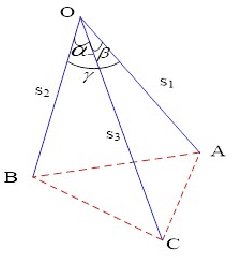
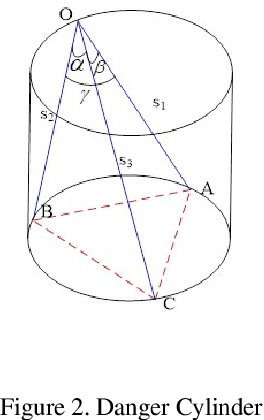
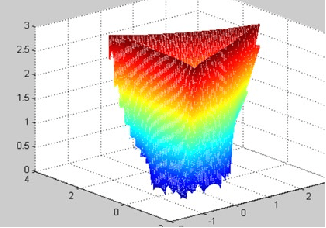
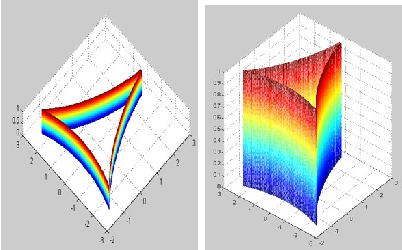
Traditionally the danger cylinder is intimately related to the solution stability in P3P problem. In this work, we show that the danger cylinder is also closely related to the multiple-solution phenomenon. More specifically, we show when the optical center lies on the danger cylinder, of the 3 possible P3P solutions, i.e., one double solution, and two other solutions, the optical center of the double solution still lies on the danger cylinder, but the optical centers of the other two solutions no longer lie on the danger cylinder. And when the optical center moves on the danger cylinder, accordingly the optical centers of the two other solutions of the corresponding P3P problem form a new surface, characterized by a polynomial equation of degree 12 in the optical center coordinates, called the Companion Surface of Danger Cylinder (CSDC). That means the danger cylinder always has a companion surface. For the significance of CSDC, we show that when the optical center passes through the CSDC, the number of solutions of P3P problem must change by 2. That means CSDC acts as a delimitating surface of the P3P solution space. These new findings shed some new lights on the P3P multi-solution phenomenon, an important issue in PnP study.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge