Interpreting Adversarial Attacks and Defences using Architectures with Enhanced Interpretability

Adversarial attacks in deep learning represent a significant threat to the integrity and reliability of machine learning models. Adversarial training has been a popular defence technique against these adversarial attacks. In this work, we capitalize on a network architecture, namely Deep Linearly Gated Networks (DLGN), which has better interpretation capabilities than regular deep network architectures. Using this architecture, we interpret robust models trained using PGD adversarial training and compare them with standard training. Feature networks in DLGN act as feature extractors, making them the only medium through which an adversary can attack the model. We analyze the feature network of DLGN with fully connected layers with respect to properties like alignment of the hyperplanes, hyperplane relation with PCA, and sub-network overlap among classes and compare these properties between robust and standard models. We also consider this architecture having CNN layers wherein we qualitatively (using visualizations) and quantitatively contrast gating patterns between robust and standard models. We uncover insights into hyperplanes resembling principal components in PGD-AT and STD-TR models, with PGD-AT hyperplanes aligned farther from the data points. We use path activity analysis to show that PGD-AT models create diverse, non-overlapping active subnetworks across classes, preventing attack-induced gating overlaps. Our visualization ideas show the nature of representations learnt by PGD-AT and STD-TR models.

Closing the Gap in the Trade-off between Fair Representations and Accuracy

The rapid developments of various machine learning models and their deployments in several applications has led to discussions around the importance of looking beyond the accuracies of these models. Fairness of such models is one such aspect that is deservedly gaining more attention. In this work, we analyse the natural language representations of documents and sentences (i.e., encodings) for any embedding-level bias that could potentially also affect the fairness of the downstream tasks that rely on them. We identify bias in these encodings either towards or against different sub-groups based on the difference in their reconstruction errors along various subsets of principal components. We explore and recommend ways to mitigate such bias in the encodings while also maintaining a decent accuracy in classification models that use them.

Byzantine Spectral Ranking

We study the problem of rank aggregation where the goal is to obtain a global ranking by aggregating pair-wise comparisons of voters over a set of items. We consider an adversarial setting where the voters are partitioned into two sets. The first set votes in a stochastic manner according to the popular score-based Bradley-Terry-Luce (BTL) model for pairwise comparisons. The second set comprises malicious Byzantine voters trying to deteriorate the ranking. We consider a strongly-adversarial scenario where the Byzantine voters know the BTL scores, the votes of the good voters, the algorithm, and can collude with each other. We first show that the popular spectral ranking based Rank-Centrality algorithm, though optimal for the BTL model, does not perform well even when a small constant fraction of the voters are Byzantine. We introduce the Byzantine Spectral Ranking Algorithm (and a faster variant of it), which produces a reliable ranking when the number of good voters exceeds the number of Byzantine voters. We show that no algorithm can produce a satisfactory ranking with probability > 1/2 for all BTL weights when there are more Byzantine voters than good voters, showing that our algorithm works for all possible population fractions. We support our theoretical results with experimental results on synthetic and real datasets to demonstrate the failure of the Rank-Centrality algorithm under several adversarial scenarios and how the proposed Byzantine Spectral Ranking algorithm is robust in obtaining good rankings.

Explicitising The Implicit Intrepretability of Deep Neural Networks Via Duality

Recent work by Lakshminarayanan and Singh [2020] provided a dual view for fully connected deep neural networks (DNNs) with rectified linear units (ReLU). It was shown that (i) the information in the gates is analytically characterised by a kernel called the neural path kernel (NPK) and (ii) most critical information is learnt in the gates, in that, given the learnt gates, the weights can be retrained from scratch without significant loss in performance. Using the dual view, in this paper, we rethink the conventional interpretations of DNNs thereby explicitsing the implicit interpretability of DNNs. Towards this, we first show new theoretical properties namely rotational invariance and ensemble structure of the NPK in the presence of convolutional layers and skip connections respectively. Our theory leads to two surprising empirical results that challenge conventional wisdom: (i) the weights can be trained even with a constant 1 input, (ii) the gating masks can be shuffled, without any significant loss in performance. These results motivate a novel class of networks which we call deep linearly gated networks (DLGNs). DLGNs using the phenomenon of dual lifting pave way to more direct and simpler interpretation of DNNs as opposed to conventional interpretations. We show via extensive experiments on CIFAR-10 and CIFAR-100 that these DLGNs lead to much better interpretability-accuracy tradeoff.

A Theory of Tournament Representations

Real world tournaments are almost always intransitive. Recent works have noted that parametric models which assume $d$ dimensional node representations can effectively model intransitive tournaments. However, nothing is known about the structure of the class of tournaments that arise out of any fixed $d$ dimensional representations. In this work, we develop a novel theory for understanding parametric tournament representations. Our first contribution is to structurally characterize the class of tournaments that arise out of $d$ dimensional representations. We do this by showing that these tournament classes have forbidden configurations which must necessarily be union of flip classes, a novel way to partition the set of all tournaments. We further characterise rank $2$ tournaments completely by showing that the associated forbidden flip class contains just $2$ tournaments. Specifically, we show that the rank $2$ tournaments are equivalent to locally-transitive tournaments. This insight allows us to show that the minimum feedback arc set problem on this tournament class can be solved using the standard Quicksort procedure. For a general rank $d$ tournament class, we show that the flip class associated with a coned-doubly regular tournament of size $\mathcal{O}(\sqrt{d})$ must be a forbidden configuration. To answer a dual question, using a celebrated result of \cite{forster}, we show a lower bound of $\mathcal{O}(\sqrt{n})$ on the minimum dimension needed to represent all tournaments on $n$ nodes. For any given tournament, we show a novel upper bound on the smallest representation dimension that depends on the least size of the number of unique nodes in any feedback arc set of the flip class associated with a tournament. We show how our results also shed light on upper bound of sign-rank of matrices.

Sequential Ski Rental Problem

The classical 'buy or rent' ski-rental problem was recently considered in the setting where multiple experts (such as Machine Learning algorithms) advice on the length of the ski season. Here, robust algorithms were developed with improved theoretical performance over adversarial scenarios where such expert predictions were unavailable. We consider a variant of this problem which we call the 'sequential ski-rental' problem. Here, a sequence of ski-rental problems has to be solved in an online fashion where both the buy cost and the length of the ski season are unknown to the learner. The learner has access to two sets of experts, one set who advise on the true cost of buying the ski and another set who advise on the length of the ski season. Under certain stochastic assumptions on the experts who predict the buy costs, we develop online algorithms and prove regret bounds for the same. Our experimental evaluations confirm our theoretical results.

Censored Semi-Bandits for Resource Allocation

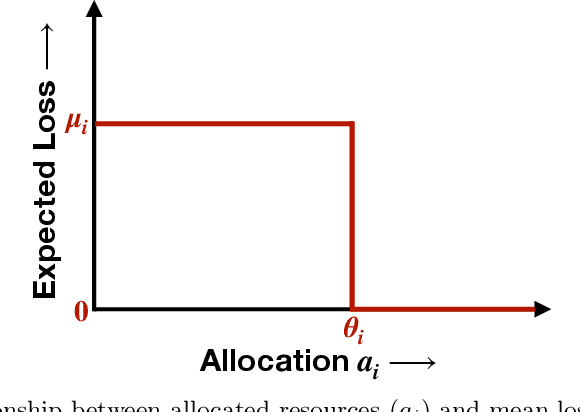
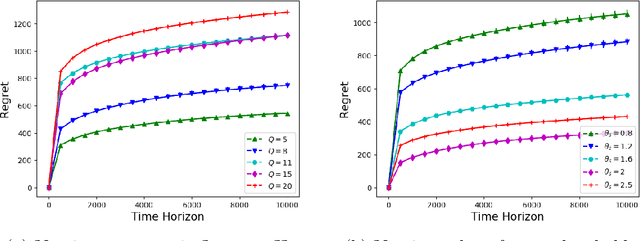
We consider the problem of sequentially allocating resources in a censored semi-bandits setup, where the learner allocates resources at each step to the arms and observes loss. The loss depends on two hidden parameters, one specific to the arm but independent of the resource allocation, and the other depends on the allocated resource. More specifically, the loss equals zero for an arm if the resource allocated to it exceeds a constant (but unknown) arm dependent threshold. The goal is to learn a resource allocation that minimizes the expected loss. The problem is challenging because the loss distribution and threshold value of each arm are unknown. We study this setting by establishing its `equivalence' to Multiple-Play Multi-Armed Bandits (MP-MAB) and Combinatorial Semi-Bandits. Exploiting these equivalences, we derive optimal algorithms for our problem setting using known algorithms for MP-MAB and Combinatorial Semi-Bandits. The experiments on synthetically generated data validate the performance guarantees of the proposed algorithms.

SUPAID: A Rule mining based method for automatic rollout decision aid for supervisors in fleet management systems

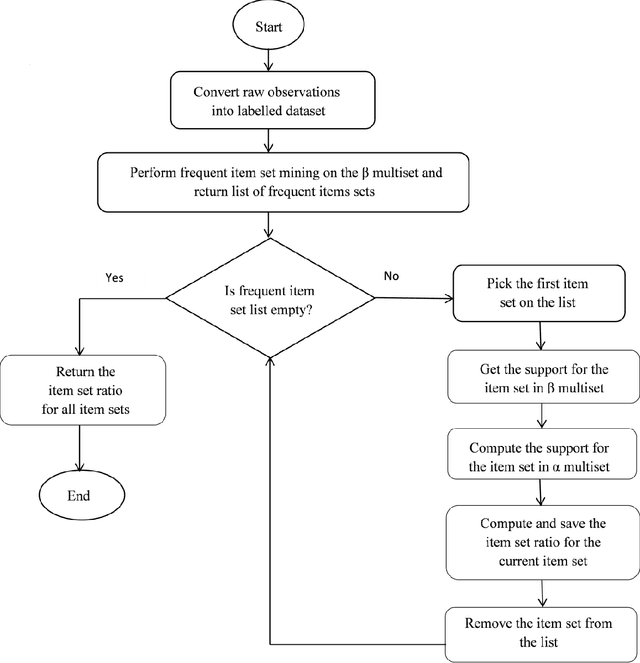
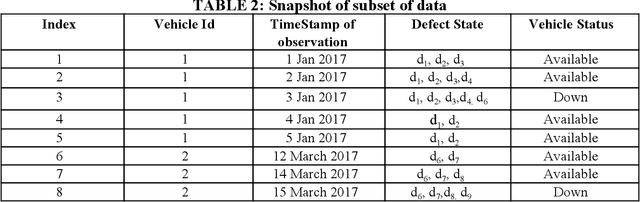
The decision to rollout a vehicle is critical to fleet management companies as wrong decisions can lead to additional cost of maintenance and failures during journey. With the availability of large amount of data and advancement of machine learning techniques, the rollout decisions of a supervisor can be effectively automated and the mistakes in decisions made by the supervisor learnt. In this paper, we propose a novel learning algorithm SUPAID which under a natural 'one-way efficiency' assumption on the supervisor, uses a rule mining approach to rank the vehicles based on their roll-out feasibility thus helping prevent the supervisor from makingerroneous decisions. Our experimental results on real data from a public transit agency from a city in U.S show that the proposed method SUPAID can result in significant cost savings.

Censored Semi-Bandits: A Framework for Resource Allocation with Censored Feedback

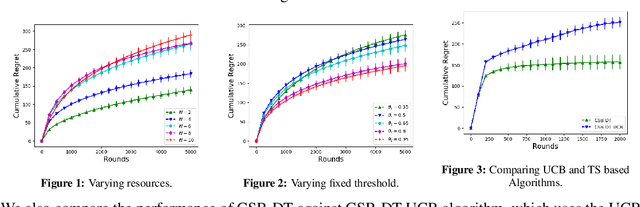
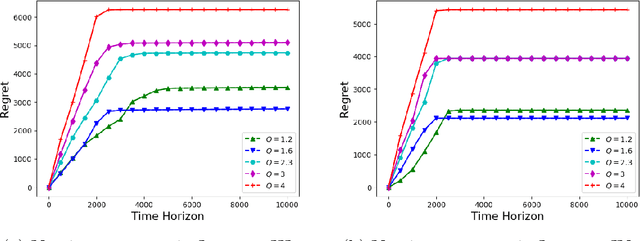
In this paper, we study Censored Semi-Bandits, a novel variant of the semi-bandits problem. The learner is assumed to have a fixed amount of resources, which it allocates to the arms at each time step. The loss observed from an arm is random and depends on the amount of resource allocated to it. More specifically, the loss equals zero if the allocation for the arm exceeds a constant (but unknown) threshold that can be dependent on the arm. Our goal is to learn a feasible allocation that minimizes the expected loss. The problem is challenging because the loss distribution and threshold value of each arm are unknown. We study this novel setting by establishing its `equivalence' to Multiple-Play Multi-Armed Bandits (MP-MAB) and Combinatorial Semi-Bandits. Exploiting these equivalences, we derive optimal algorithms for our setting using existing algorithms for MP-MAB and Combinatorial Semi-Bandits. Experiments on synthetically generated data validate performance guarantees of the proposed algorithms.

Ranking with Features: Algorithm and A Graph Theoretic Analysis

We consider the problem of ranking a set of items from pairwise comparisons in the presence of features associated with the items. Recent works have established that $O(n\log(n))$ samples are needed to rank well when there is no feature information present. However, this might be sub-optimal in the presence of associated features. We introduce a new probabilistic preference model called feature-Bradley-Terry-Luce (f-BTL) model that generalizes the standard BTL model to incorporate feature information. We present a new least squares based algorithm called fBTL-LS which we show requires much lesser than $O(n\log(n))$ pairs to obtain a good ranking -- precisely our new sample complexity bound is of $O(\alpha\log \alpha)$, where $\alpha$ denotes the number of `independent items' of the set, in general $\alpha << n$. Our analysis is novel and makes use of tools from classical graph matching theory to provide tighter bounds that sheds light on the true complexity of the ranking problem, capturing the item dependencies in terms of their feature representations. This was not possible with earlier matrix completion based tools used for this problem. We also prove an information theoretic lower bound on the required sample complexity for recovering the underlying ranking, which essentially shows the tightness of our proposed algorithms. The efficacy of our proposed algorithms are validated through extensive experimental evaluations on a variety of synthetic and real world datasets.