Does Order Matter : Connecting The Law of Robustness to Robust Generalization

Bubeck and Sellke (2021) pose as an open problem the connection between the law of robustness and robust generalization. The law of robustness states that overparameterization is necessary for models to interpolate robustly; in particular, robust interpolation requires the learned function to be Lipschitz. Robust generalization asks whether small robust training loss implies small robust test loss. We resolve this problem by explicitly connecting the two for arbitrary data distributions. Specifically, we introduce a nontrivial notion of robust generalization error and convert it into a lower bound on the expected Rademacher complexity of the induced robust loss class. Our bounds recover the $Ω(n^{1/d})$ regime of Wu et al. (2023) and show that, up to constants, robust generalization does not change the order of the Lipschitz constant required for smooth interpolation. We conduct experiments to probe the predicted scaling with dataset size and model capacity, testing whether empirical behavior aligns more closely with the predictions of Bubeck and Sellke (2021) or Wu et al. (2023). For MNIST, we find that the lower-bound Lipschitz constant scales on the order predicted by Wu et al. (2023). Informally, to obtain low robust generalization error, the Lipschitz constant must lie in a range that we bound, and the allowable perturbation radius is linked to the Lipschitz scale.

Physics Aware Neural Networks: Denoising for Magnetic Navigation

Magnetic-anomaly navigation, leveraging small-scale variations in the Earth's magnetic field, is a promising alternative when GPS is unavailable or compromised. Airborne systems face a key challenge in extracting geomagnetic field data: the aircraft itself induces magnetic noise. Although the classical Tolles-Lawson model addresses this, it inadequately handles stochastically corrupted magnetic data required for navigation. To address stochastic noise, we propose a framework based on two physics-based constraints: divergence-free vector field and E(3)-equivariance. These ensure the learned magnetic field obeys Maxwell's equations and that outputs transform correctly with sensor position/orientation. The divergence-free constraint is implemented by training a neural network to output a vector potential $A$, with the magnetic field defined as its curl. For E(3)-equivariance, we use tensor products of geometric tensors representable via spherical harmonics with known rotational transformations. Enforcing physical consistency and restricting the admissible function space acts as an implicit regularizer that improves spatio-temporal performance. We present ablation studies evaluating each constraint alone and jointly across CNNs, MLPs, Liquid Time Constant models, and Contiformers. Continuous-time dynamics and long-term memory are critical for modelling magnetic time series; the Contiformer architecture, which provides both, outperforms state-of-the-art methods. To mitigate data scarcity, we generate synthetic datasets using the World Magnetic Model (WMM) with time-series conditional GANs, producing realistic, temporally consistent magnetic sequences across varied trajectories and environments. Experiments show that embedding these constraints significantly improves predictive accuracy and physical plausibility, outperforming classical and unconstrained deep learning approaches.

Oscillators Are All You Need: Irregular Time Series Modelling via Damped Harmonic Oscillators with Closed-Form Solutions

Transformers excel at time series modelling through attention mechanisms that capture long-term temporal patterns. However, they assume uniform time intervals and therefore struggle with irregular time series. Neural Ordinary Differential Equations (NODEs) effectively handle irregular time series by modelling hidden states as continuously evolving trajectories. ContiFormers arxiv:2402.10635 combine NODEs with Transformers, but inherit the computational bottleneck of the former by using heavy numerical solvers. This bottleneck can be removed by using a closed-form solution for the given dynamical system - but this is known to be intractable in general! We obviate this by replacing NODEs with a novel linear damped harmonic oscillator analogy - which has a known closed-form solution. We model keys and values as damped, driven oscillators and expand the query in a sinusoidal basis up to a suitable number of modes. This analogy naturally captures the query-key coupling that is fundamental to any transformer architecture by modelling attention as a resonance phenomenon. Our closed-form solution eliminates the computational overhead of numerical ODE solvers while preserving expressivity. We prove that this oscillator-based parameterisation maintains the universal approximation property of continuous-time attention; specifically, any discrete attention matrix realisable by ContiFormer's continuous keys can be approximated arbitrarily well by our fixed oscillator modes. Our approach delivers both theoretical guarantees and scalability, achieving state-of-the-art performance on irregular time series benchmarks while being orders of magnitude faster.

Building Interpretable Models for Moral Decision-Making

We build a custom transformer model to study how neural networks make moral decisions on trolley-style dilemmas. The model processes structured scenarios using embeddings that encode who is affected, how many people, and which outcome they belong to. Our 2-layer architecture achieves 77% accuracy on Moral Machine data while remaining small enough for detailed analysis. We use different interpretability techniques to uncover how moral reasoning distributes across the network, demonstrating that biases localize to distinct computational stages among other findings.

Grokking Modular Polynomials

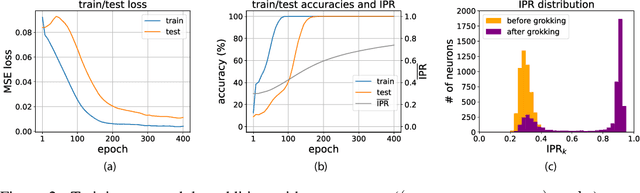
Neural networks readily learn a subset of the modular arithmetic tasks, while failing to generalize on the rest. This limitation remains unmoved by the choice of architecture and training strategies. On the other hand, an analytical solution for the weights of Multi-layer Perceptron (MLP) networks that generalize on the modular addition task is known in the literature. In this work, we (i) extend the class of analytical solutions to include modular multiplication as well as modular addition with many terms. Additionally, we show that real networks trained on these datasets learn similar solutions upon generalization (grokking). (ii) We combine these "expert" solutions to construct networks that generalize on arbitrary modular polynomials. (iii) We hypothesize a classification of modular polynomials into learnable and non-learnable via neural networks training; and provide experimental evidence supporting our claims.

Learning to grok: Emergence of in-context learning and skill composition in modular arithmetic tasks

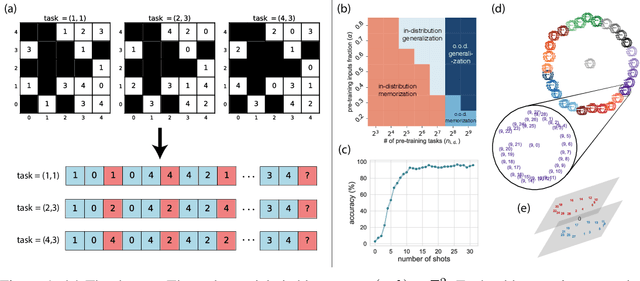
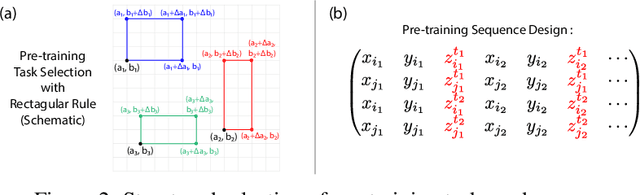
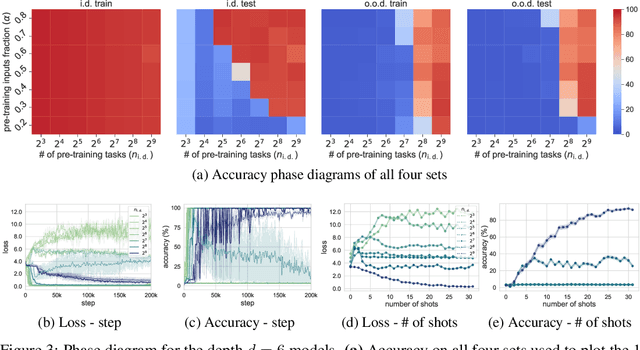
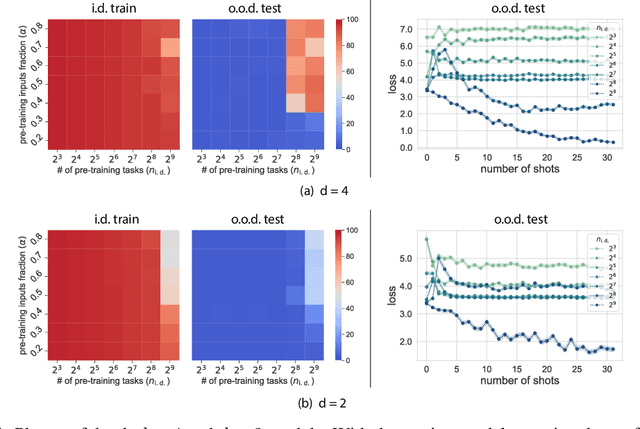
Large language models can solve tasks that were not present in the training set. This capability is believed to be due to in-context learning and skill composition. In this work, we study the emergence of in-context learning and skill composition in a collection of modular arithmetic tasks. Specifically, we consider a finite collection of linear modular functions $z = a \, x + b \, y \;\mathrm{mod}\; p$ labeled by the vector $(a, b) \in \mathbb{Z}_p^2$. We use some of these tasks for pre-training and the rest for out-of-distribution testing. We empirically show that a GPT-style transformer exhibits a transition from in-distribution to out-of-distribution generalization as the number of pre-training tasks increases. We find that the smallest model capable of out-of-distribution generalization requires two transformer blocks, while for deeper models, the out-of-distribution generalization phase is \emph{transient}, necessitating early stopping. Finally, we perform an interpretability study of the pre-trained models, revealing the highly structured representations in both phases; and discuss the learnt algorithm.

To grok or not to grok: Disentangling generalization and memorization on corrupted algorithmic datasets

Robust generalization is a major challenge in deep learning, particularly when the number of trainable parameters is very large. In general, it is very difficult to know if the network has memorized a particular set of examples or understood the underlying rule (or both). Motivated by this challenge, we study an interpretable model where generalizing representations are understood analytically, and are easily distinguishable from the memorizing ones. Namely, we consider two-layer neural networks trained on modular arithmetic tasks where ($\xi \cdot 100\%$) of labels are corrupted (\emph{i.e.} some results of the modular operations in the training set are incorrect). We show that (i) it is possible for the network to memorize the corrupted labels \emph{and} achieve $100\%$ generalization at the same time; (ii) the memorizing neurons can be identified and pruned, lowering the accuracy on corrupted data and improving the accuracy on uncorrupted data; (iii) regularization methods such as weight decay, dropout and BatchNorm force the network to ignore the corrupted data during optimization, and achieve $100\%$ accuracy on the uncorrupted dataset; and (iv) the effect of these regularization methods is (``mechanistically'') interpretable: weight decay and dropout force all the neurons to learn generalizing representations, while BatchNorm de-amplifies the output of memorizing neurons and amplifies the output of the generalizing ones. Finally, we show that in the presence of regularization, the training dynamics involves two consecutive stages: first, the network undergoes the \emph{grokking} dynamics reaching high train \emph{and} test accuracy; second, it unlearns the memorizing representations, where train accuracy suddenly jumps from $100\%$ to $100 (1-\xi)\%$.

Combining Multi-level Contexts of Superpixel using Convolutional Neural Networks to perform Natural Scene Labeling

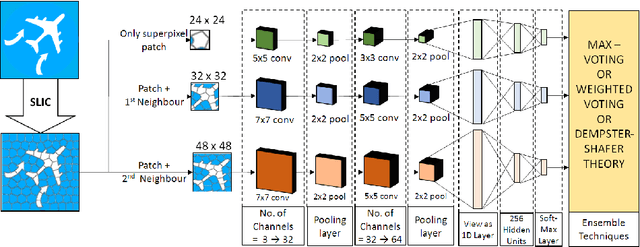
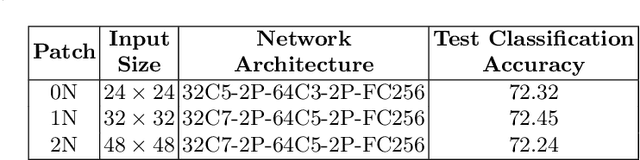
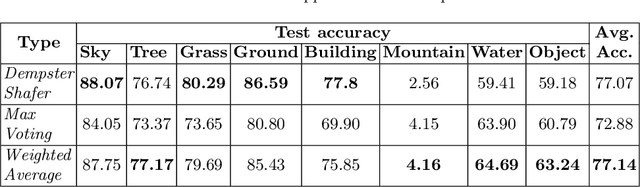
Modern deep learning algorithms have triggered various image segmentation approaches. However most of them deal with pixel based segmentation. However, superpixels provide a certain degree of contextual information while reducing computation cost. In our approach, we have performed superpixel level semantic segmentation considering 3 various levels as neighbours for semantic contexts. Furthermore, we have enlisted a number of ensemble approaches like max-voting and weighted-average. We have also used the Dempster-Shafer theory of uncertainty to analyze confusion among various classes. Our method has proved to be superior to a number of different modern approaches on the same dataset.