Inducing Multi-Convexity in Path Constrained Trajectory Optimization for Mobile Manipulators

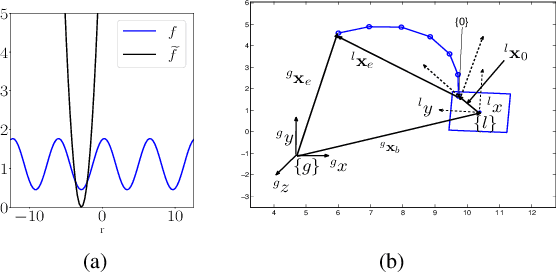
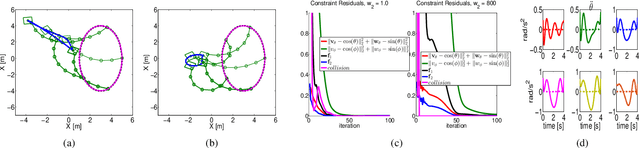
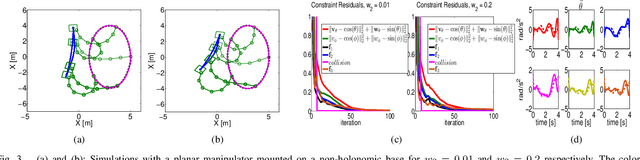
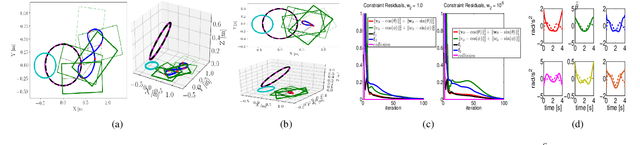
In this paper, we propose a novel trajectory optimization algorithm for mobile manipulators under end-effector path, collision avoidance and various kinematic constraints. Our key contribution lies in showing how this highly non-linear and non-convex problem can be solved as a sequence of convex unconstrained quadratic programs (QPs). This is achieved by reformulating the non-linear constraints that arise out of manipulator kinematics and its coupling with the mobile base in a multi-affine form. We then use techniques from Alternating Direction Method of Multipliers (ADMM) to formulate and solve the trajectory optimization problem. The proposed ADMM has two similar non-convex steps. Importantly, a convex surrogate can be derived for each of them. We show how large parts of our optimization can be solved in parallel providing the possibility of exploiting multi-core CPUs/GPUs. We validate our trajectory optimization on different benchmark examples. Specifically, we highlight how it solves the cyclicity bottleneck and provides a holistic approach where diverse set of trajectories can be obtained by trading-off different aspects of manipulator and mobile base motion.

Combining Method of Alternating Projections and Augmented Lagrangian for Task Constrained Trajectory Optimization

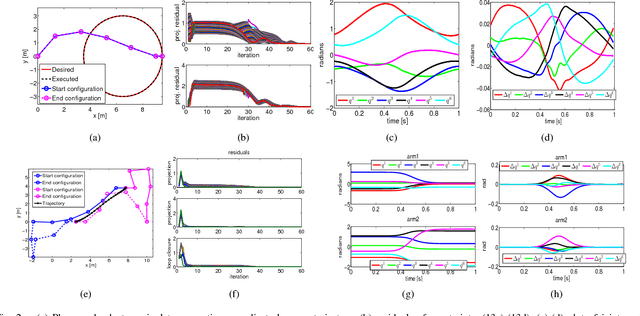
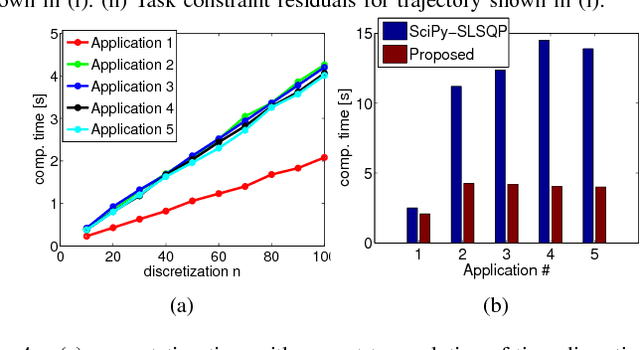
Motion planning for manipulators under task space constraints is difficult as it constrains the joint configurations to always lie on an implicitly defined manifold. It is possible to view task constrained motion planning as an optimization problem with non-linear equality constraints which can be solved by general non-linear optimization techniques. In this paper, we present a novel custom optimizer which exploits the underlying structure present in many task constraints. At the core of our approach are some simple reformulations, which when coupled with the \emph{method of alternating projection}, leads to an efficient convex optimization based routine for computing a feasible solution to the task constraints. We subsequently build on this result and use the concept of Augmented Lagrangian to guide the feasible solutions towards those which also minimize the user defined cost function. We show that the proposed optimizer is fully distributive and thus, can be easily parallelized. We validate our formulation on some common robotic benchmark problems. In particular, we show that the proposed optimizer achieves cyclic motion in the joint space corresponding to a similar nature trajectory in the task space. Furthermore, as a baseline, we compare the proposed optimizer with an off-the-shelf non-linear solver provide in open source package SciPy. We show that for similar task constraint residuals and smoothness cost, it can be upto more than three times faster than the SciPy alternative.

Machine Learning for Neuroimaging with Scikit-Learn

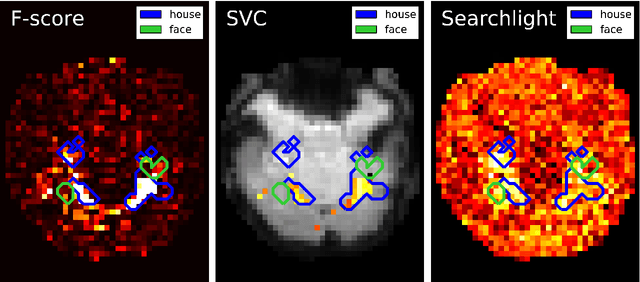
Statistical machine learning methods are increasingly used for neuroimaging data analysis. Their main virtue is their ability to model high-dimensional datasets, e.g. multivariate analysis of activation images or resting-state time series. Supervised learning is typically used in decoding or encoding settings to relate brain images to behavioral or clinical observations, while unsupervised learning can uncover hidden structures in sets of images (e.g. resting state functional MRI) or find sub-populations in large cohorts. By considering different functional neuroimaging applications, we illustrate how scikit-learn, a Python machine learning library, can be used to perform some key analysis steps. Scikit-learn contains a very large set of statistical learning algorithms, both supervised and unsupervised, and its application to neuroimaging data provides a versatile tool to study the brain.