Andrei Ahonen
Inducing Multi-Convexity in Path Constrained Trajectory Optimization for Mobile Manipulators
Apr 22, 2019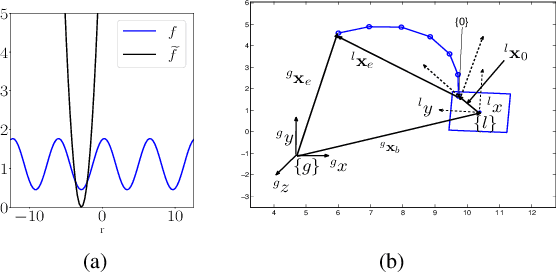
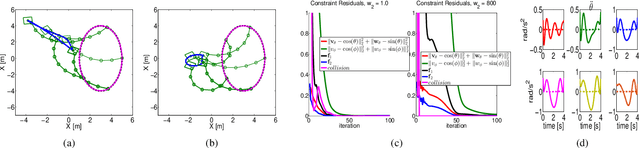
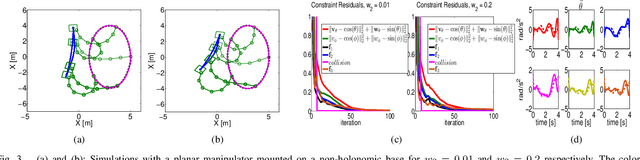
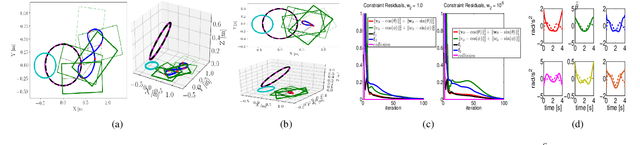
Abstract:In this paper, we propose a novel trajectory optimization algorithm for mobile manipulators under end-effector path, collision avoidance and various kinematic constraints. Our key contribution lies in showing how this highly non-linear and non-convex problem can be solved as a sequence of convex unconstrained quadratic programs (QPs). This is achieved by reformulating the non-linear constraints that arise out of manipulator kinematics and its coupling with the mobile base in a multi-affine form. We then use techniques from Alternating Direction Method of Multipliers (ADMM) to formulate and solve the trajectory optimization problem. The proposed ADMM has two similar non-convex steps. Importantly, a convex surrogate can be derived for each of them. We show how large parts of our optimization can be solved in parallel providing the possibility of exploiting multi-core CPUs/GPUs. We validate our trajectory optimization on different benchmark examples. Specifically, we highlight how it solves the cyclicity bottleneck and provides a holistic approach where diverse set of trajectories can be obtained by trading-off different aspects of manipulator and mobile base motion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge