Reliability of CKA as a Similarity Measure in Deep Learning

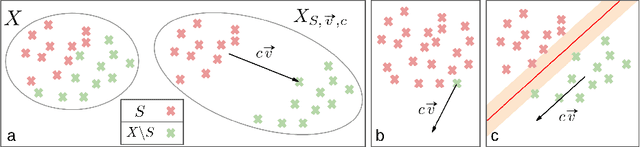
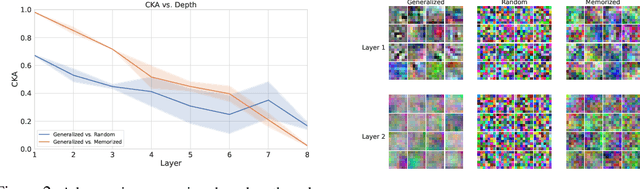
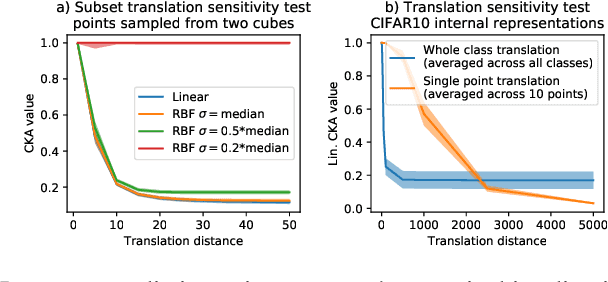
Comparing learned neural representations in neural networks is a challenging but important problem, which has been approached in different ways. The Centered Kernel Alignment (CKA) similarity metric, particularly its linear variant, has recently become a popular approach and has been widely used to compare representations of a network's different layers, of architecturally similar networks trained differently, or of models with different architectures trained on the same data. A wide variety of conclusions about similarity and dissimilarity of these various representations have been made using CKA. In this work we present analysis that formally characterizes CKA sensitivity to a large class of simple transformations, which can naturally occur in the context of modern machine learning. This provides a concrete explanation of CKA sensitivity to outliers, which has been observed in past works, and to transformations that preserve the linear separability of the data, an important generalization attribute. We empirically investigate several weaknesses of the CKA similarity metric, demonstrating situations in which it gives unexpected or counter-intuitive results. Finally we study approaches for modifying representations to maintain functional behaviour while changing the CKA value. Our results illustrate that, in many cases, the CKA value can be easily manipulated without substantial changes to the functional behaviour of the models, and call for caution when leveraging activation alignment metrics.

Embedding Signals on Knowledge Graphs with Unbalanced Diffusion Earth Mover's Distance

In modern relational machine learning it is common to encounter large graphs that arise via interactions or similarities between observations in many domains. Further, in many cases the target entities for analysis are actually signals on such graphs. We propose to compare and organize such datasets of graph signals by using an earth mover's distance (EMD) with a geodesic cost over the underlying graph. Typically, EMD is computed by optimizing over the cost of transporting one probability distribution to another over an underlying metric space. However, this is inefficient when computing the EMD between many signals. Here, we propose an unbalanced graph earth mover's distance that efficiently embeds the unbalanced EMD on an underlying graph into an $L^1$ space, whose metric we call unbalanced diffusion earth mover's distance (UDEMD). This leads us to an efficient nearest neighbors kernel over many signals defined on a large graph. Next, we show how this gives distances between graph signals that are robust to noise. Finally, we apply this to organizing patients based on clinical notes who are modelled as signals on the SNOMED-CT medical knowledge graph, embedding lymphoblast cells modeled as signals on a gene graph, and organizing genes modeled as signals over a large peripheral blood mononuclear (PBMC) cell graph. In each case, we show that UDEMD-based embeddings find accurate distances that are highly efficient compared to other methods.

Diffusion Earth Mover's Distance and Distribution Embeddings

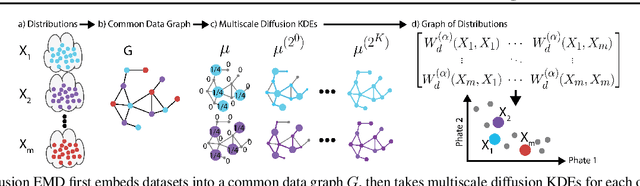
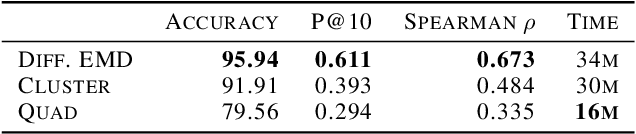
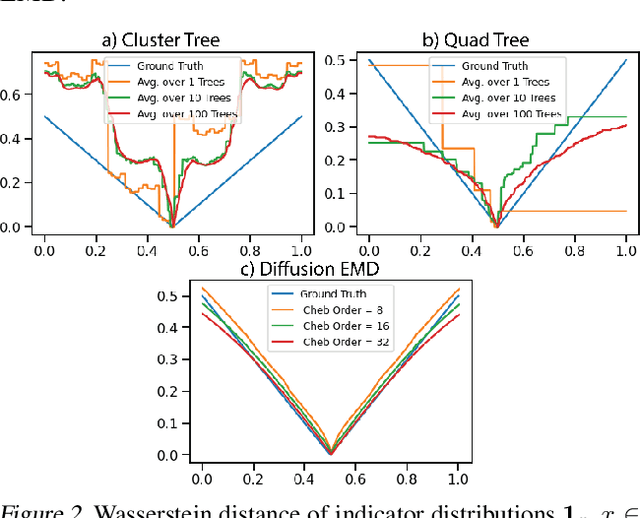
We propose a new fast method of measuring distances between large numbers of related high dimensional datasets called the Diffusion Earth Mover's Distance (EMD). We model the datasets as distributions supported on common data graph that is derived from the affinity matrix computed on the combined data. In such cases where the graph is a discretization of an underlying Riemannian closed manifold, we prove that Diffusion EMD is topologically equivalent to the standard EMD with a geodesic ground distance. Diffusion EMD can be computed in $\tilde{O}(n)$ time and is more accurate than similarly fast algorithms such as tree-based EMDs. We also show Diffusion EMD is fully differentiable, making it amenable to future uses in gradient-descent frameworks such as deep neural networks. Finally, we demonstrate an application of Diffusion EMD to single cell data collected from 210 COVID-19 patient samples at Yale New Haven Hospital. Here, Diffusion EMD can derive distances between patients on the manifold of cells at least two orders of magnitude faster than equally accurate methods. This distance matrix between patients can be embedded into a higher level patient manifold which uncovers structure and heterogeneity in patients. More generally, Diffusion EMD is applicable to all datasets that are massively collected in parallel in many medical and biological systems.