PRIEST: Projection Guided Sampling-Based Optimization For Autonomous Navigation

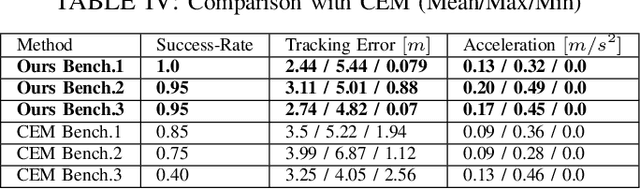
Efficient navigation in unknown and dynamic environments is crucial for expanding the application domain of mobile robots. The core challenge stems from the nonavailability of a feasible global path for guiding optimization-based local planners. As a result, existing local planners often get trapped in poor local minima. In this paper, we present a novel optimizer that can explore multiple homotopies to plan high-quality trajectories over long horizons while still being fast enough for real-time applications. We build on the gradient-free paradigm by augmenting the trajectory sampling strategy with a projection optimization that guides the samples toward a feasible region. As a result, our approach can recover from the frequently encountered pathological cases wherein all the sampled trajectories lie in the high-cost region. Furthermore, we also show that our projection optimization has a highly parallelizable structure that can be easily accelerated over GPUs. We push the state-of-the-art in the following respects. Over the navigation stack of the Robot Operating System (ROS), we show an improvement of 7-13% in success rate and up to two times in total travel time metric. On the same benchmarks and metrics, our approach achieves up to 44% improvement over MPPI and its recent variants. On simple point-to-point navigation tasks, our optimizer is up to two times more reliable than SOTA gradient-based solvers, as well as sampling-based approaches such as the Cross-Entropy Method (CEM) and VPSTO. Codes: https://github.com/fatemeh-rastgar/PRIEST

GPU Accelerated Batch Multi-Convex Trajectory Optimization for a Rectangular Holonomic Mobile Robot

We present a batch trajectory optimizer that can simultaneously solve hundreds of different instances of the problem in real-time. We consider holonomic robots but relax the assumption of circular base footprint. Our main algorithmic contributions lie in: (i) improving the computational tractability of the underlying non-convex problem and (ii) leveraging batch computation to mitigate initialization bottlenecks and improve solution quality. We achieve both goals by deriving a multi-convex reformulation of the kinematics and collision avoidance constraints. We exploit these structures through an Alternating Minimization approach and show that the resulting batch operation reduces to computing just matrix-vector products that can be trivially accelerated over GPUs. We improve the state-of-the-art in three respects. First, we improve quality of navigation (success-rate, tracking) as compared to baseline approach that relies on computing a single locally optimal trajectory at each control loop. Second, we show that when initialized with trajectory samples from a Gaussian distribution, our batch optimizer outperforms state-of-the-art cross-entropy method in solution quality. Finally, our batch optimizer is several orders of magnitude faster than the conceptually simpler alternative of running different optimization instances in parallel CPU threads. \textbf{Codes:} \url{https://tinyurl.com/a3b99m8}

GPU Accelerated Convex Approximations for Fast Multi-Agent Trajectory Optimization

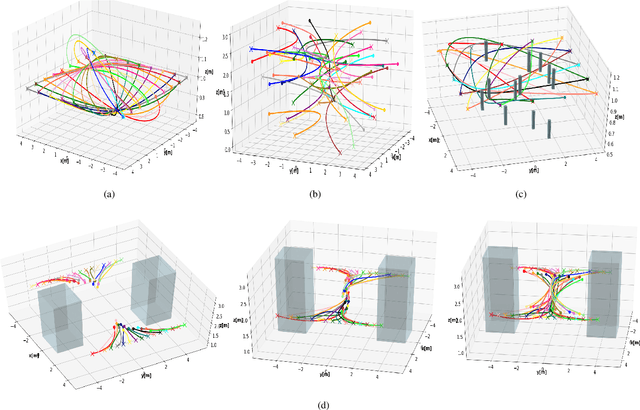
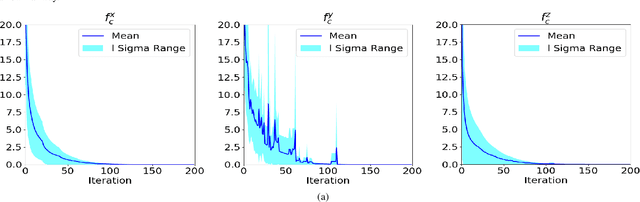
In this paper, we present a computationally efficient trajectory optimizer that can exploit GPUs to jointly compute trajectories of tens of agents in under a second. At the heart of our optimizer is a novel reformulation of the non-convex collision avoidance constraints that reduces the core computation in each iteration to that of solving a large scale, convex, unconstrained Quadratic Program (QP). We also show that the matrix factorization/inverse computation associated with the QP needs to be done only once and can be done offline for a given number of agents. This further simplifies the solution process, effectively reducing it to a problem of evaluating a few matrix-vector products. Moreover, for a large number of agents, this computation can be trivially accelerated on GPUs using existing off-the-shelf libraries. We validate our optimizer's performance on challenging benchmarks and show substantial improvement over state of the art in computation time and trajectory quality.