GPU Accelerated Convex Approximations for Fast Multi-Agent Trajectory Optimization
Paper and Code
Nov 09, 2020

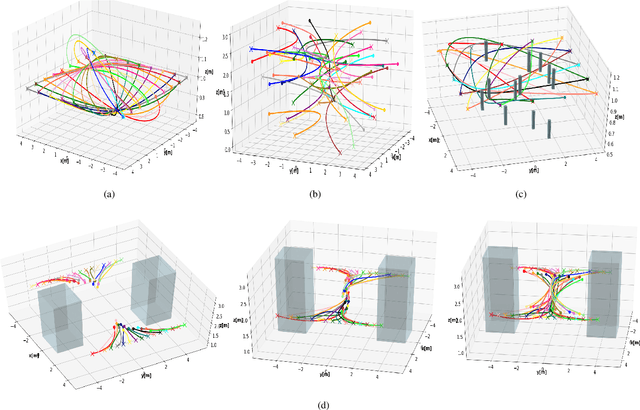
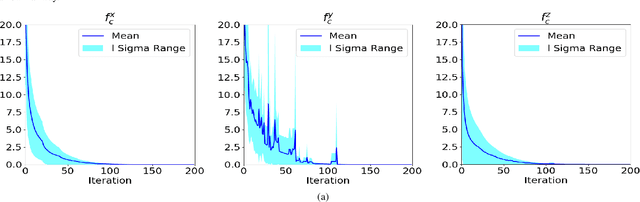
In this paper, we present a computationally efficient trajectory optimizer that can exploit GPUs to jointly compute trajectories of tens of agents in under a second. At the heart of our optimizer is a novel reformulation of the non-convex collision avoidance constraints that reduces the core computation in each iteration to that of solving a large scale, convex, unconstrained Quadratic Program (QP). We also show that the matrix factorization/inverse computation associated with the QP needs to be done only once and can be done offline for a given number of agents. This further simplifies the solution process, effectively reducing it to a problem of evaluating a few matrix-vector products. Moreover, for a large number of agents, this computation can be trivially accelerated on GPUs using existing off-the-shelf libraries. We validate our optimizer's performance on challenging benchmarks and show substantial improvement over state of the art in computation time and trajectory quality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge