Real-Time Multi-Convex Model Predictive Control for Occlusion Free Target Tracking

This paper proposes a Model Predictive Control (MPC) algorithm for target tracking amongst static and dynamic obstacles. Our main contribution lies in improving the computational tractability and reliability of the underlying non-convex trajectory optimization. The result is an MPC algorithm that runs real-time on laptops and embedded hardware devices such as Jetson TX2. Our approach relies on novel reformulations for the tracking, collision, and occlusion constraints that induce a multi-convex structure in the resulting trajectory optimization. We exploit these mathematical structures using the split Bregman Iteration technique, eventually reducing our MPC to a series of convex Quadratic Programs solvable in a few milliseconds. The fast re-planning of our MPC allows for occlusion and collision-free tracking in complex environments even while considering a simple constant-velocity prediction for the target trajectory and dynamic obstacles. We perform extensive bench-marking in a realistic physics engine and show that our MPC outperforms the state-of-the-art algorithms in visibility, smoothness, and computation-time metrics.

Embedded Hardware Appropriate Fast 3D Trajectory Optimization for Fixed Wing Aerial Vehicles by Leveraging Hidden Convex Structures

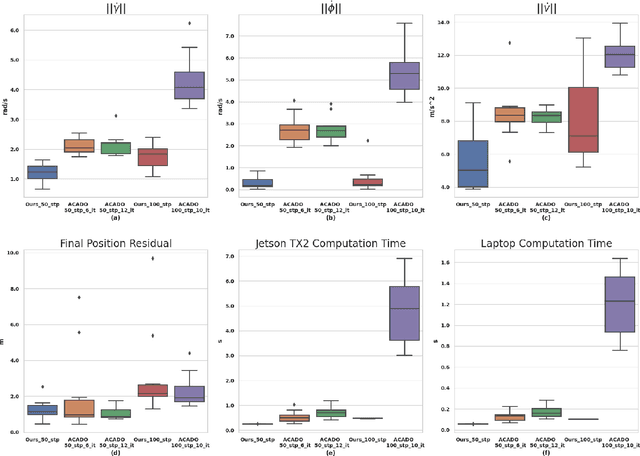
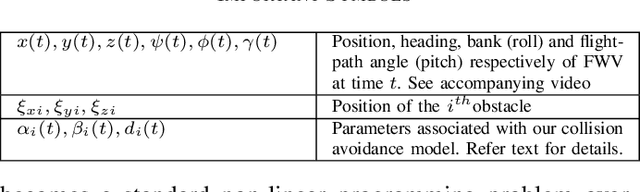
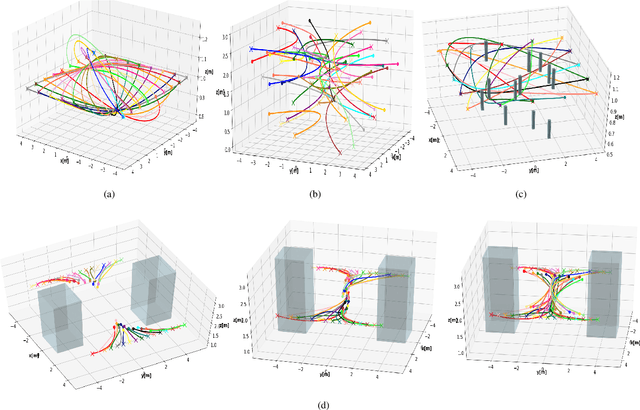
Most commercially available fixed-wing aerial vehicles (FWV) can carry only small, lightweight computing hardware such as Jetson TX2 onboard. Solving non-linear trajectory optimization on these computing resources is computationally challenging even while considering only the kinematic motion model. Most importantly, the computation time increases sharply as the environment becomes more cluttered. In this paper, we take a step towards overcoming this bottleneck and propose a trajectory optimizer that achieves online performance on both conventional laptops/desktops and Jetson TX2 in a typical urban environment setting. Our optimizer builds on the novel insight that the seemingly non-linear trajectory optimization problem for FWV has an implicit multi-convex structure. Our optimizer exploits these computational structures by bringing together diverse concepts from Alternating Minimization, Bregman iteration, and Alternating Direction Method of Multipliers. We show that our optimizer outperforms the state-of-the-art implementation of sequential quadratic programming approach in optimal control solver ACADO in computation time and solution quality measured in terms of control and goal reaching cost.

GPU Accelerated Convex Approximations for Fast Multi-Agent Trajectory Optimization

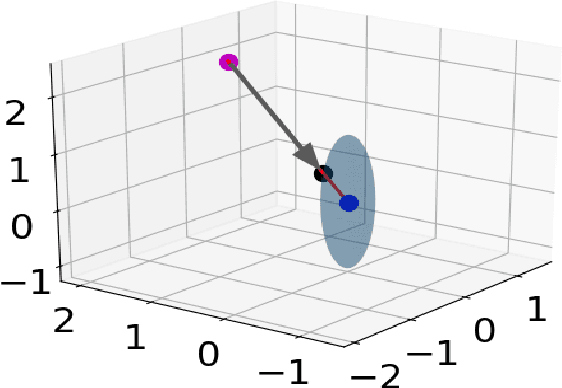
In this paper, we present a computationally efficient trajectory optimizer that can exploit GPUs to jointly compute trajectories of tens of agents in under a second. At the heart of our optimizer is a novel reformulation of the non-convex collision avoidance constraints that reduces the core computation in each iteration to that of solving a large scale, convex, unconstrained Quadratic Program (QP). We also show that the matrix factorization/inverse computation associated with the QP needs to be done only once and can be done offline for a given number of agents. This further simplifies the solution process, effectively reducing it to a problem of evaluating a few matrix-vector products. Moreover, for a large number of agents, this computation can be trivially accelerated on GPUs using existing off-the-shelf libraries. We validate our optimizer's performance on challenging benchmarks and show substantial improvement over state of the art in computation time and trajectory quality.