JEN-1: Text-Guided Universal Music Generation with Omnidirectional Diffusion Models

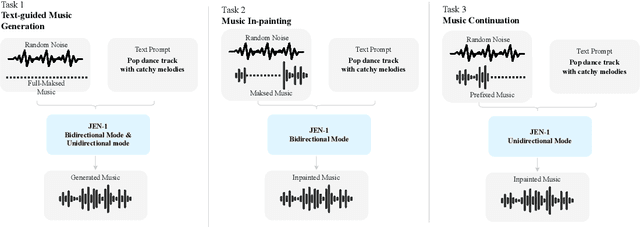
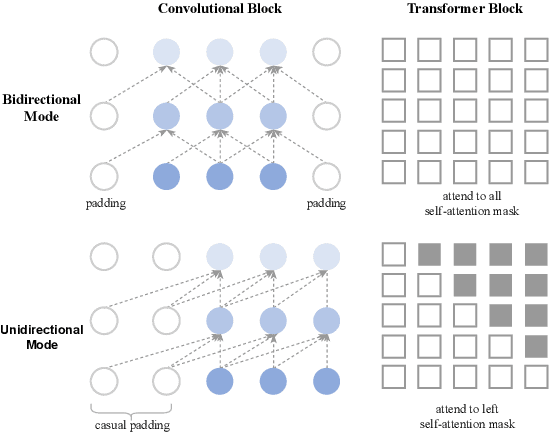
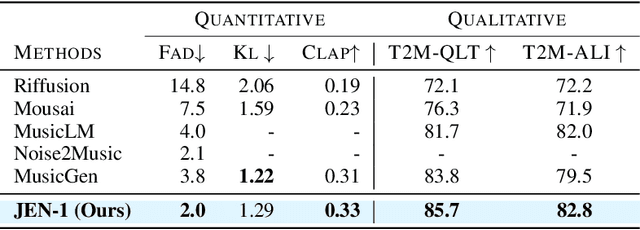
Music generation has attracted growing interest with the advancement of deep generative models. However, generating music conditioned on textual descriptions, known as text-to-music, remains challenging due to the complexity of musical structures and high sampling rate requirements. Despite the task's significance, prevailing generative models exhibit limitations in music quality, computational efficiency, and generalization. This paper introduces JEN-1, a universal high-fidelity model for text-to-music generation. JEN-1 is a diffusion model incorporating both autoregressive and non-autoregressive training. Through in-context learning, JEN-1 performs various generation tasks including text-guided music generation, music inpainting, and continuation. Evaluations demonstrate JEN-1's superior performance over state-of-the-art methods in text-music alignment and music quality while maintaining computational efficiency. Our demos are available at http://futureverse.com/research/jen/demos/jen1

Fast nonlinear risk assessment for autonomous vehicles using learned conditional probabilistic models of agent futures

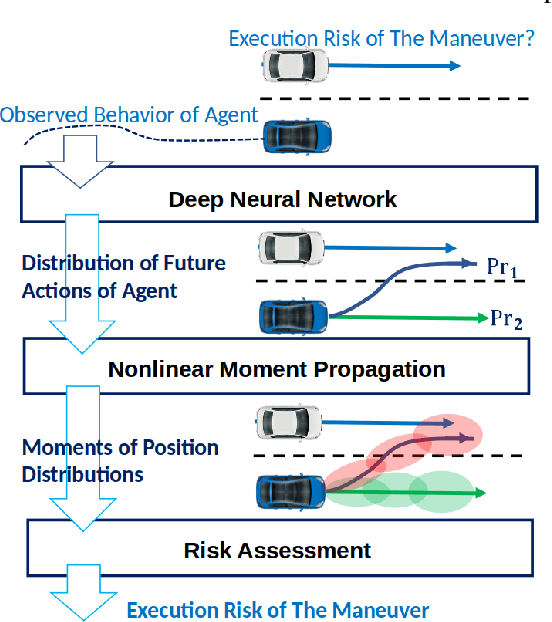
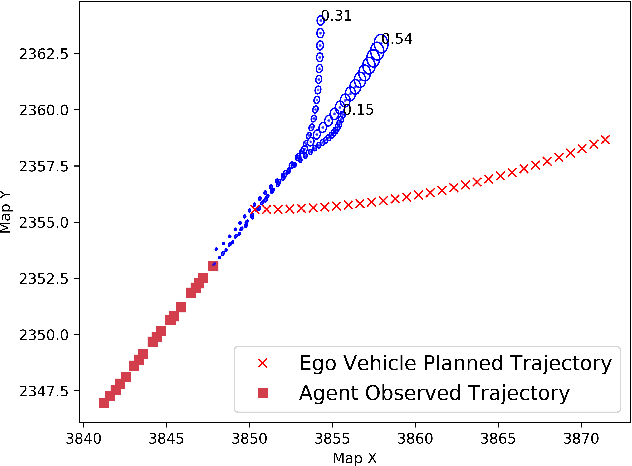
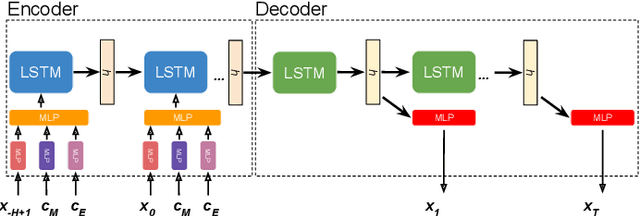
This paper presents fast non-sampling based methods to assess the risk for trajectories of autonomous vehicles when probabilistic predictions of other agents' futures are generated by deep neural networks (DNNs). The presented methods address a wide range of representations for uncertain predictions including both Gaussian and non-Gaussian mixture models to predict both agent positions and control inputs conditioned on the scene contexts. We show that the problem of risk assessment when Gaussian mixture models (GMMs) of agent positions are learned can be solved rapidly to arbitrary levels of accuracy with existing numerical methods. To address the problem of risk assessment for non-Gaussian mixture models of agent position, we propose finding upper bounds on risk using nonlinear Chebyshev's Inequality and sums-of-squares (SOS) programming; they are both of interest as the former is much faster while the latter can be arbitrarily tight. These approaches only require higher order statistical moments of agent positions to determine upper bounds on risk. To perform risk assessment when models are learned for agent control inputs as opposed to positions, we propagate the moments of uncertain control inputs through the nonlinear motion dynamics to obtain the exact moments of uncertain position over the planning horizon. To this end, we construct deterministic linear dynamical systems that govern the exact time evolution of the moments of uncertain position in the presence of uncertain control inputs. The presented methods are demonstrated on realistic predictions from DNNs trained on the Argoverse and CARLA datasets and are shown to be effective for rapidly assessing the probability of low probability events.

Moment-Based Exact Uncertainty Propagation Through Nonlinear Stochastic Autonomous Systems

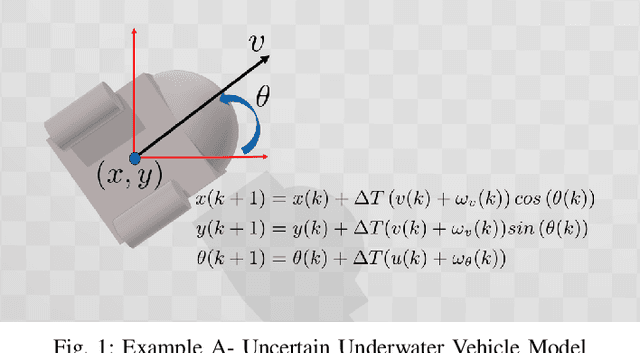
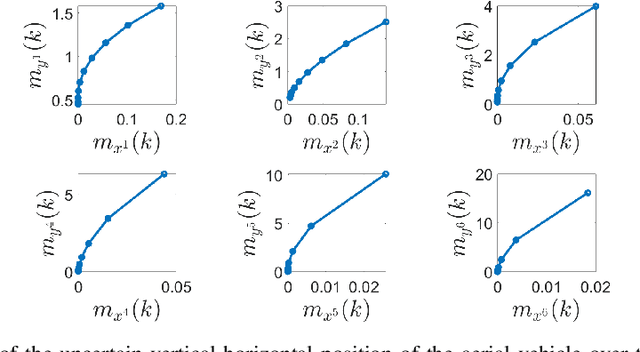
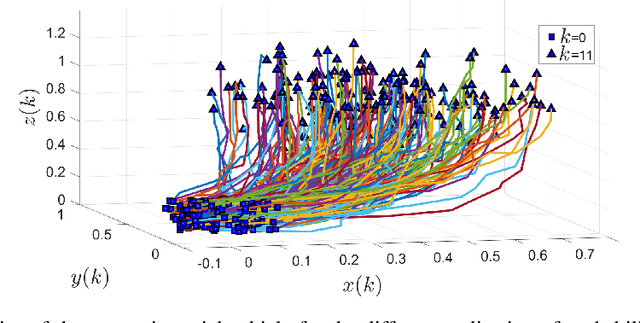
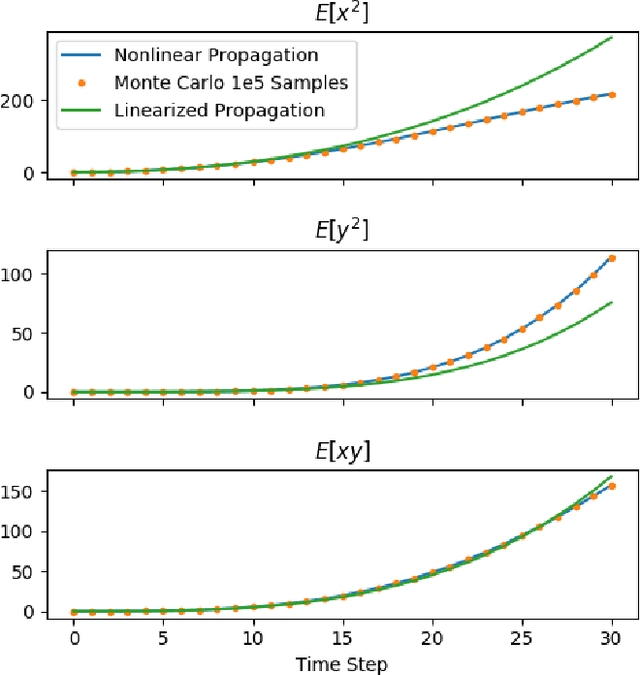
In this paper, we address the problem of uncertainty propagation through nonlinear stochastic dynamical systems. More precisely, given a discrete-time continuous-state probabilistic nonlinear dynamical system, we aim at finding the sequence of the moments of the probability distributions of the system states up to any desired order over the given planning horizon. Moments of uncertain states can be used in estimation, planning, control, and safety analysis of stochastic dynamical systems. Existing approaches to address moment propagation problems provide approximate descriptions of the moments and are mainly limited to particular set of uncertainties, e.g., Gaussian disturbances. In this paper, to describe the moments of uncertain states, we introduce trigonometric and also mixed-trigonometric-polynomial moments. Such moments allow us to obtain closed deterministic dynamical systems that describe the exact time evolution of the moments of uncertain states of an important class of autonomous and robotic systems including underwater, ground, and aerial vehicles, robotic arms and walking robots. Such obtained deterministic dynamical systems can be used, in a receding horizon fashion, to propagate the uncertainties over the planning horizon in real-time. To illustrate the performance of the proposed method, we benchmark our method against existing approaches including linear, unscented transformation, and sampling based uncertainty propagation methods that are widely used in estimation, prediction, planning, and control problems.

Fast Risk Assessment for Autonomous Vehicles Using Learned Models of Agent Futures

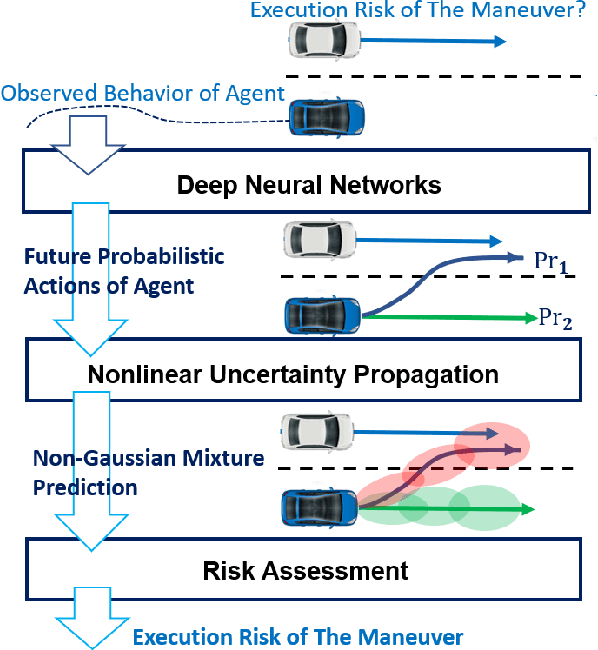
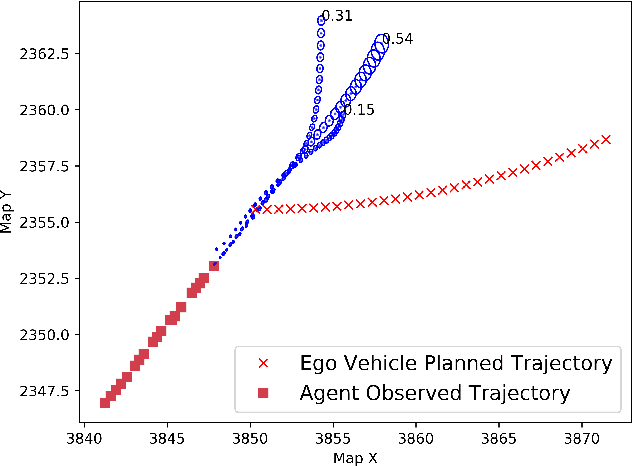
This paper presents fast non-sampling based methods to assess the risk of trajectories for autonomous vehicles when probabilistic predictions of other agents' futures are generated by deep neural networks (DNNs). The presented methods address a wide range of representations for uncertain predictions including both Gaussian and non-Gaussian mixture models for predictions of both agent positions and controls. We show that the problem of risk assessment when Gaussian mixture models (GMMs) of agent positions are learned can be solved rapidly to arbitrary levels of accuracy with existing numerical methods. To address the problem of risk assessment for non-Gaussian mixture models of agent position, we propose finding upper bounds on risk using Chebyshev's Inequality and sums-of-squares (SOS) programming; they are both of interest as the former is much faster while the latter can be arbitrarily tight. These approaches only require statistical moments of agent positions to determine upper bounds on risk. To perform risk assessment when models are learned for agent controls as opposed to positions, we develop TreeRing, an algorithm analogous to tree search over the ring of polynomials that can be used to exactly propagate moments of control distributions into position distributions through nonlinear dynamics. The presented methods are demonstrated on realistic predictions from DNNs trained on the Argoverse and CARLA datasets and are shown to be effective for rapidly assessing the probability of low probability events.

Moment State Dynamical Systems for Nonlinear Chance-Constrained Motion Planning

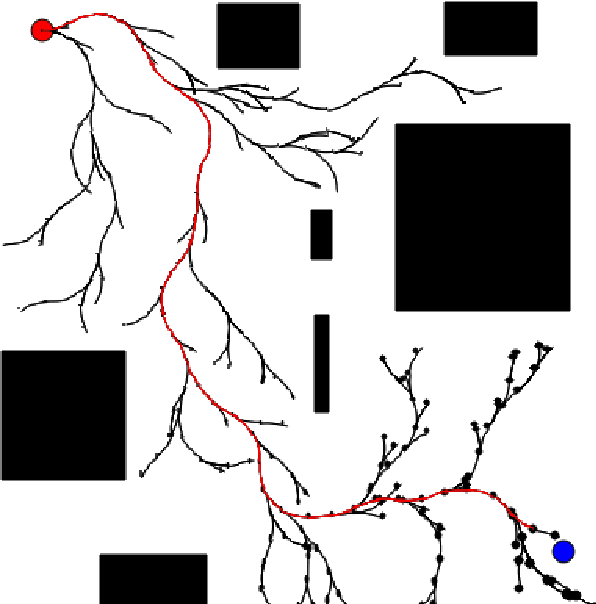
Chance-constrained motion planning requires uncertainty in dynamics to be propagated into uncertainty in state. When nonlinear models are used, Gaussian assumptions on the state distribution do not necessarily apply since almost all random variables propagated through nonlinear dynamics results in non-Gaussian state distributions. To address this, recent works have developed moment-based approaches for enforcing chance-constraints on non-Gaussian state distributions. However, there still lacks fast and accurate moment propagation methods to determine the necessary statistical moments of these state distributions. To address this gap, we present a framework that, given a stochastic dynamical system, can algorithmically search for a new dynamical system in terms of moment state that can be used to propagate moments of disturbance random variables into moments of the state distribution. The key algorithm, TreeRing, can be applied to a large class of nonlinear systems which we refer to as trigonometric polynomial systems. As an example application, we present a distributionally robust RRT (DR-RRT) algorithm that propagates uncertainty through the nonlinear Dubin's car model without linearization.

Non-Gaussian Chance-Constrained Trajectory Planning for Autonomous Vehicles in the Presence of Uncertain Agents

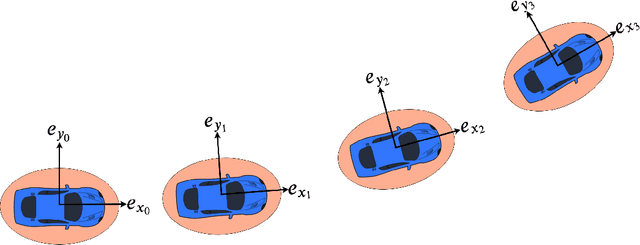
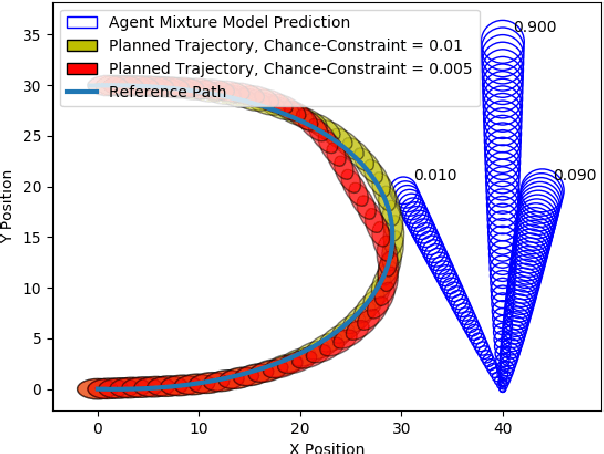
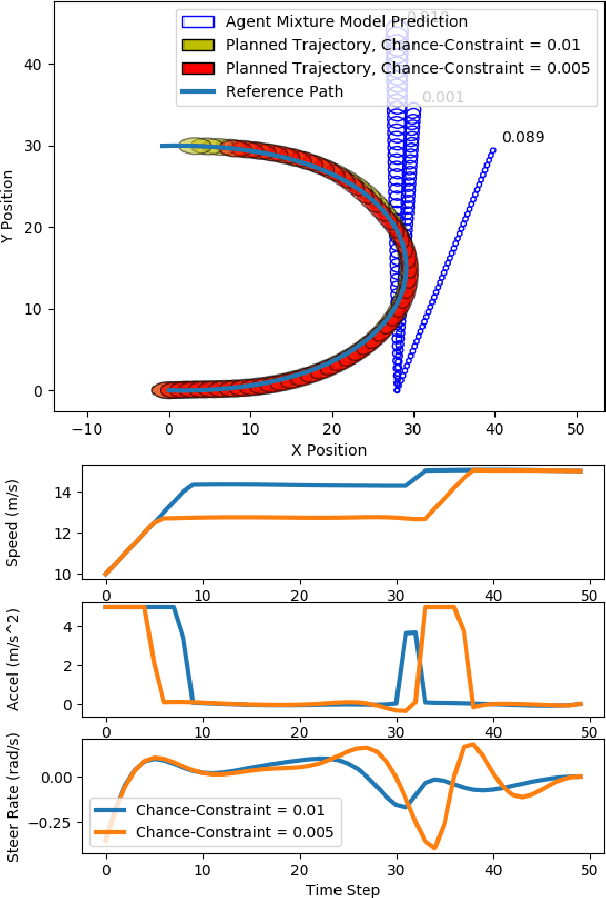
Agent behavior is arguably the greatest source of uncertainty in trajectory planning for autonomous vehicles. This problem has motivated significant amounts of work in the behavior prediction community on learning rich distributions of the future states and actions of agents. However, most current work in trajectory planning in the presence of uncertain agents or obstacles is limited to the case of Gaussian uncertainty, which is a limited representation, or requires sampling, which can be computationally intractable to encode in an optimization problem. In this paper, we present a general method for enforcing chance-constraints on the probability of collision with other agents in model predictive control problems for autonomous driving that can be used with non-Gaussian mixture models of agent positions. Our method involves using statistical moments of the non-Gaussian distributions to enforce Cantelli's Inequality, which we show can upper bound the probability of collision. We then demonstrate its application to chance-constrained trajectory planning using model predictive contouring control. In experiments, we show that the resulting optimization problem can be solved with state-of-the-art nonlinear program (NLP) solvers to plan trajectories with 5 second horizons in real-time.