Moment State Dynamical Systems for Nonlinear Chance-Constrained Motion Planning
Paper and Code
Mar 28, 2020
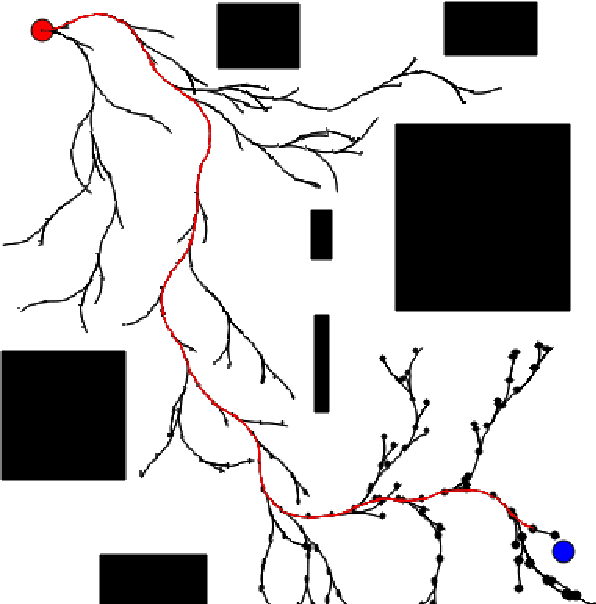
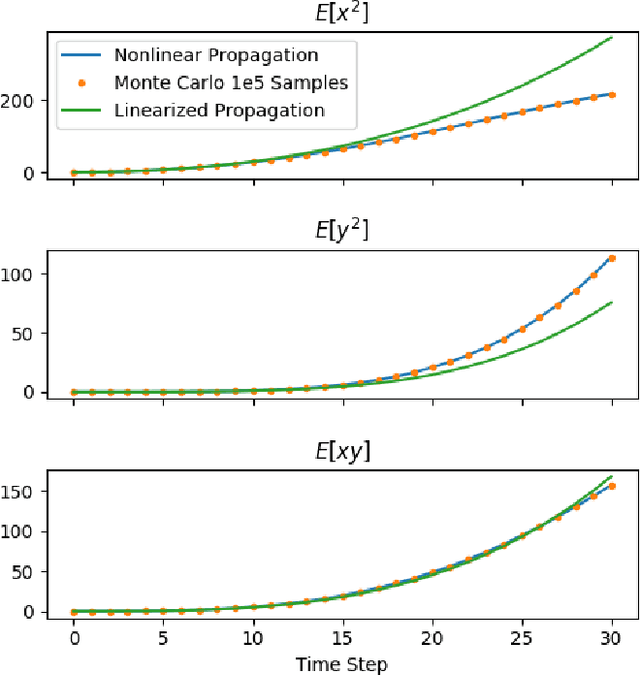
Chance-constrained motion planning requires uncertainty in dynamics to be propagated into uncertainty in state. When nonlinear models are used, Gaussian assumptions on the state distribution do not necessarily apply since almost all random variables propagated through nonlinear dynamics results in non-Gaussian state distributions. To address this, recent works have developed moment-based approaches for enforcing chance-constraints on non-Gaussian state distributions. However, there still lacks fast and accurate moment propagation methods to determine the necessary statistical moments of these state distributions. To address this gap, we present a framework that, given a stochastic dynamical system, can algorithmically search for a new dynamical system in terms of moment state that can be used to propagate moments of disturbance random variables into moments of the state distribution. The key algorithm, TreeRing, can be applied to a large class of nonlinear systems which we refer to as trigonometric polynomial systems. As an example application, we present a distributionally robust RRT (DR-RRT) algorithm that propagates uncertainty through the nonlinear Dubin's car model without linearization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge