Non-Gaussian Chance-Constrained Trajectory Planning for Autonomous Vehicles in the Presence of Uncertain Agents
Paper and Code
Mar 01, 2020
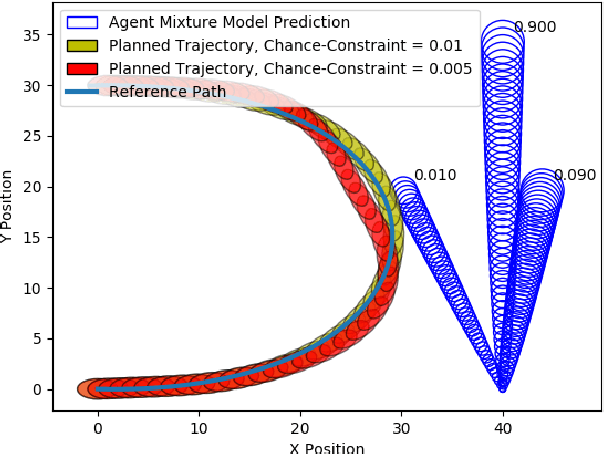
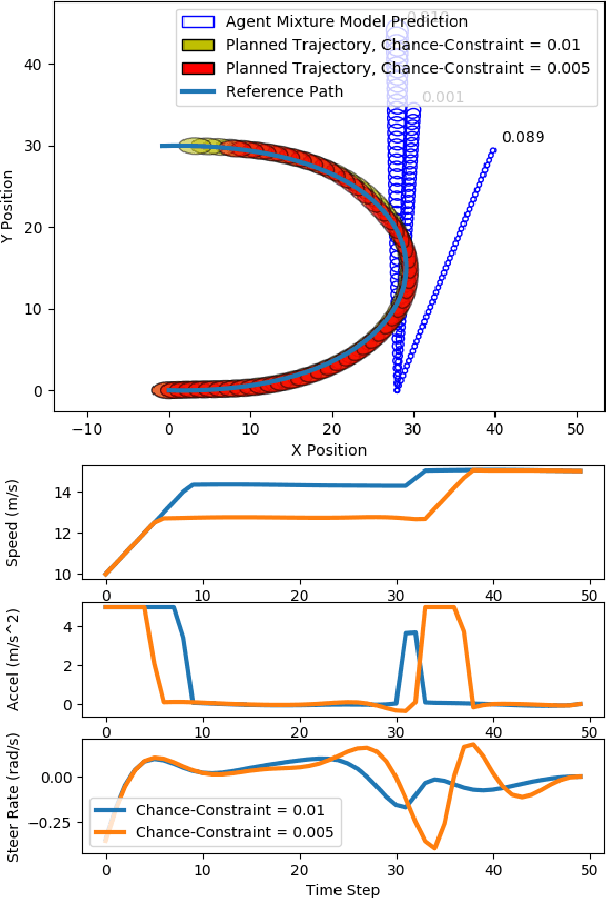

Agent behavior is arguably the greatest source of uncertainty in trajectory planning for autonomous vehicles. This problem has motivated significant amounts of work in the behavior prediction community on learning rich distributions of the future states and actions of agents. However, most current work in trajectory planning in the presence of uncertain agents or obstacles is limited to the case of Gaussian uncertainty, which is a limited representation, or requires sampling, which can be computationally intractable to encode in an optimization problem. In this paper, we present a general method for enforcing chance-constraints on the probability of collision with other agents in model predictive control problems for autonomous driving that can be used with non-Gaussian mixture models of agent positions. Our method involves using statistical moments of the non-Gaussian distributions to enforce Cantelli's Inequality, which we show can upper bound the probability of collision. We then demonstrate its application to chance-constrained trajectory planning using model predictive contouring control. In experiments, we show that the resulting optimization problem can be solved with state-of-the-art nonlinear program (NLP) solvers to plan trajectories with 5 second horizons in real-time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge