Fast Risk Assessment for Autonomous Vehicles Using Learned Models of Agent Futures
Paper and Code
Jun 03, 2020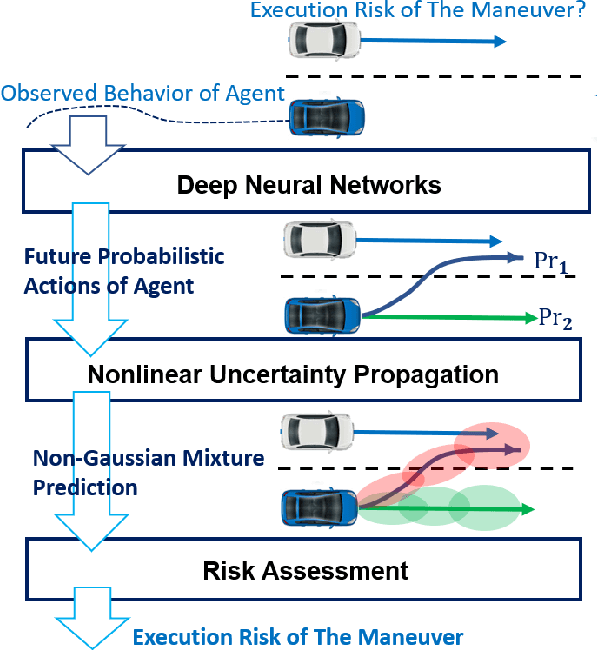
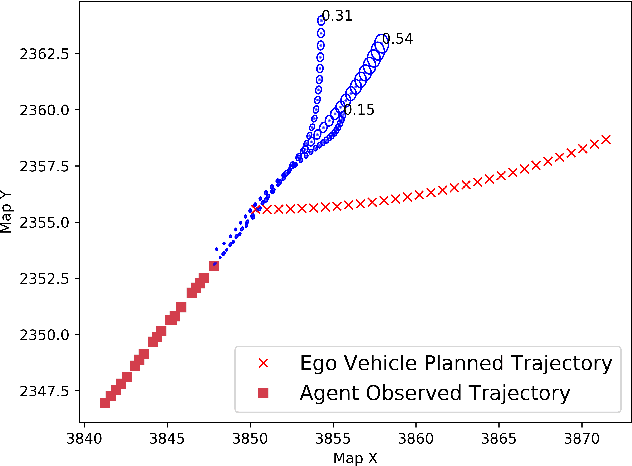


This paper presents fast non-sampling based methods to assess the risk of trajectories for autonomous vehicles when probabilistic predictions of other agents' futures are generated by deep neural networks (DNNs). The presented methods address a wide range of representations for uncertain predictions including both Gaussian and non-Gaussian mixture models for predictions of both agent positions and controls. We show that the problem of risk assessment when Gaussian mixture models (GMMs) of agent positions are learned can be solved rapidly to arbitrary levels of accuracy with existing numerical methods. To address the problem of risk assessment for non-Gaussian mixture models of agent position, we propose finding upper bounds on risk using Chebyshev's Inequality and sums-of-squares (SOS) programming; they are both of interest as the former is much faster while the latter can be arbitrarily tight. These approaches only require statistical moments of agent positions to determine upper bounds on risk. To perform risk assessment when models are learned for agent controls as opposed to positions, we develop TreeRing, an algorithm analogous to tree search over the ring of polynomials that can be used to exactly propagate moments of control distributions into position distributions through nonlinear dynamics. The presented methods are demonstrated on realistic predictions from DNNs trained on the Argoverse and CARLA datasets and are shown to be effective for rapidly assessing the probability of low probability events.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge