Moment-Based Exact Uncertainty Propagation Through Nonlinear Stochastic Autonomous Systems
Paper and Code
Jan 29, 2021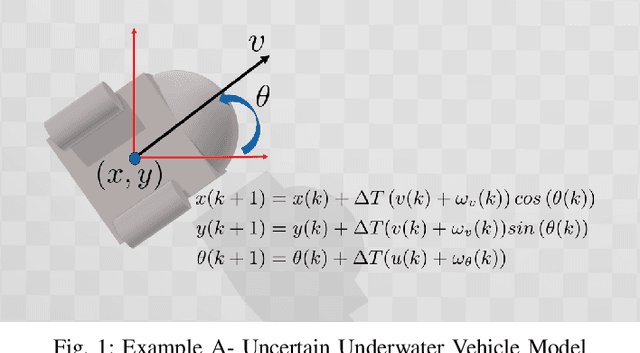
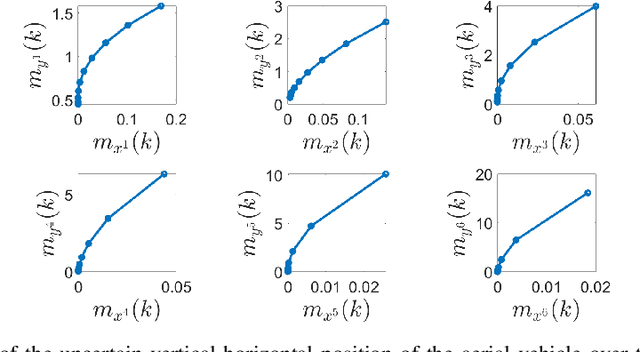

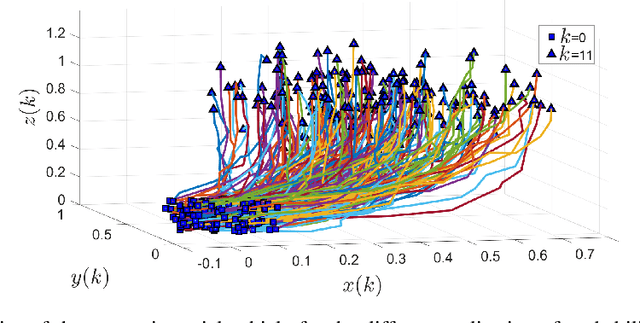
In this paper, we address the problem of uncertainty propagation through nonlinear stochastic dynamical systems. More precisely, given a discrete-time continuous-state probabilistic nonlinear dynamical system, we aim at finding the sequence of the moments of the probability distributions of the system states up to any desired order over the given planning horizon. Moments of uncertain states can be used in estimation, planning, control, and safety analysis of stochastic dynamical systems. Existing approaches to address moment propagation problems provide approximate descriptions of the moments and are mainly limited to particular set of uncertainties, e.g., Gaussian disturbances. In this paper, to describe the moments of uncertain states, we introduce trigonometric and also mixed-trigonometric-polynomial moments. Such moments allow us to obtain closed deterministic dynamical systems that describe the exact time evolution of the moments of uncertain states of an important class of autonomous and robotic systems including underwater, ground, and aerial vehicles, robotic arms and walking robots. Such obtained deterministic dynamical systems can be used, in a receding horizon fashion, to propagate the uncertainties over the planning horizon in real-time. To illustrate the performance of the proposed method, we benchmark our method against existing approaches including linear, unscented transformation, and sampling based uncertainty propagation methods that are widely used in estimation, prediction, planning, and control problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge