Inverse Constrained Reinforcement Learning

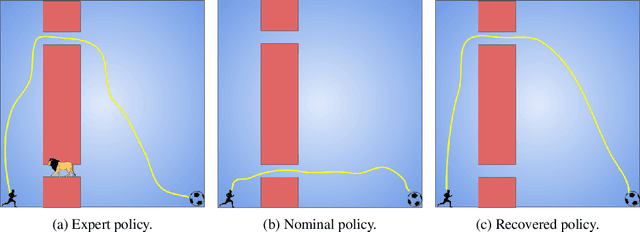
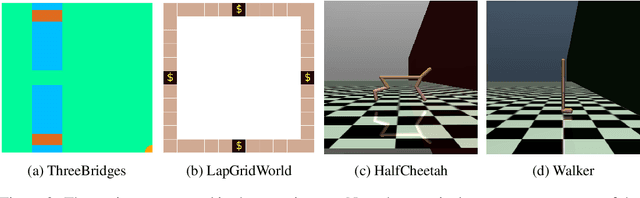
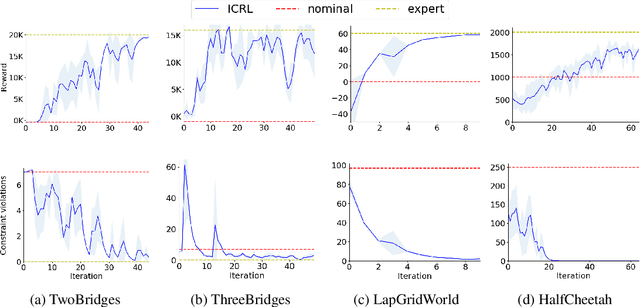
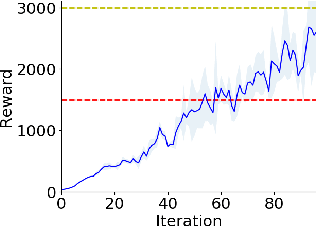
Standard reinforcement learning (RL) algorithms train agents to maximize given reward functions. However, many real-world applications of RL require agents to also satisfy certain constraints which may, for example, be motivated by safety concerns. Constrained RL algorithms approach this problem by training agents to maximize given reward functions while respecting \textit{explicitly} defined constraints. However, in many cases, manually designing accurate constraints is a challenging task. In this work, given a reward function and a set of demonstrations from an expert that maximizes this reward function while respecting \textit{unknown} constraints, we propose a framework to learn the most likely constraints that the expert respects. We then train agents to maximize the given reward function subject to the learned constraints. Previous works in this regard have either mainly been restricted to tabular settings or specific types of constraints or assume knowledge of transition dynamics of the environment. In contrast, we empirically show that our framework is able to learn arbitrary \textit{Markovian} constraints in high-dimensions in a model-free setting.

Subsampled Fourier Ptychography using Pretrained Invertible and Untrained Network Priors

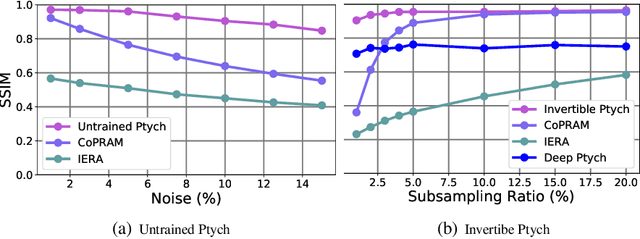
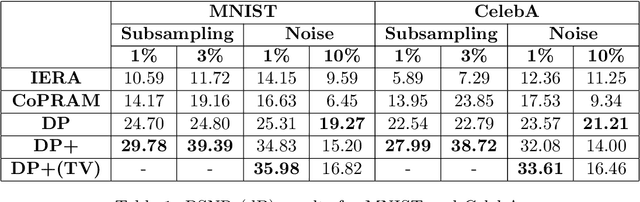
Recently pretrained generative models have shown promising results for subsampled Fourier Ptychography (FP) in terms of quality of reconstruction for extremely low sampling rate and high noise. However, one of the significant drawbacks of these pretrained generative priors is their limited representation capabilities. Moreover, training these generative models requires access to a large number of fully-observed clean samples of a particular class of images like faces or digits that is prohibitive to obtain in the context of FP. In this paper, we propose to leverage the power of pretrained invertible and untrained generative models to mitigate the representation error issue and requirement of a large number of example images (for training generative models) respectively. Through extensive experiments, we demonstrate the effectiveness of proposed approaches in the context of FP for low sampling rates and high noise levels.

Learning To Solve Differential Equations Across Initial Conditions

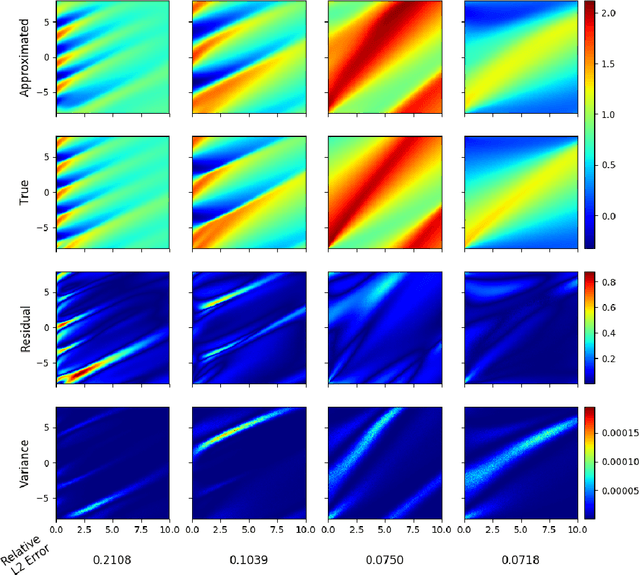
Recently, there has been a lot of interest in using neural networks for solving partial differential equations. A number of neural network-based partial differential equation solvers have been formulated which provide performances equivalent, and in some cases even superior, to classical solvers. However, these neural solvers, in general, need to be retrained each time the initial conditions or the domain of the partial differential equation changes. In this work, we posit the problem of approximating the solution of a fixed partial differential equation for any arbitrary initial conditions as learning a conditional probability distribution. We demonstrate the utility of our method on Burger's Equation.

Class-Specific Blind Deconvolutional Phase Retrieval Under a Generative Prior

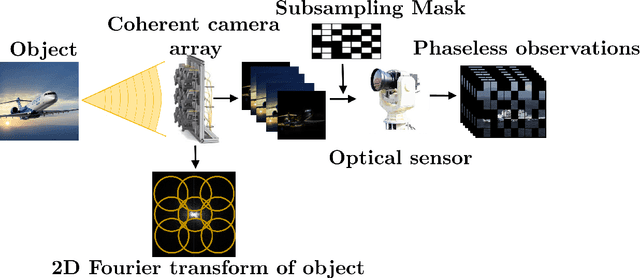
In this paper, we consider the highly ill-posed problem of jointly recovering two real-valued signals from the phaseless measurements of their circular convolution. The problem arises in various imaging modalities such as Fourier ptychography, X-ray crystallography, and in visible light communication. We propose to solve this inverse problem using alternating gradient descent algorithm under two pretrained deep generative networks as priors; one is trained on sharp images and the other on blur kernels. The proposed recovery algorithm strives to find a sharp image and a blur kernel in the range of the respective pre-generators that \textit{best} explain the forward measurement model. In doing so, we are able to reconstruct quality image estimates. Moreover, the numerics show that the proposed approach performs well on the challenging measurement models that reflect the physically realizable imaging systems and is also robust to noise

Blind Image Deconvolution using Pretrained Generative Priors

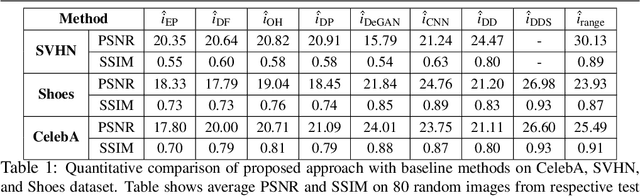
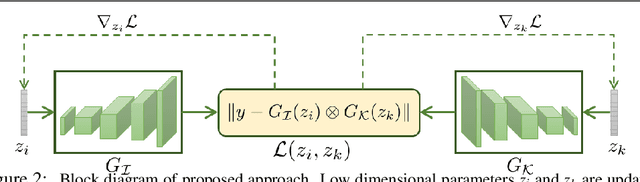
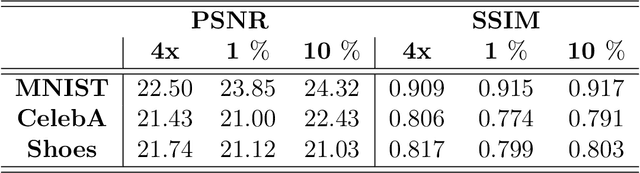
This paper proposes a novel approach to regularize the ill-posed blind image deconvolution (blind image deblurring) problem using deep generative networks. We employ two separate deep generative models - one trained to produce sharp images while the other trained to generate blur kernels from lower dimensional parameters. To deblur, we propose an alternating gradient descent scheme operating in the latent lower-dimensional space of each of the pretrained generative models. Our experiments show excellent deblurring results even under large blurs and heavy noise. To improve the performance on rich image datasets not well learned by the generative networks, we present a modification of the proposed scheme that governs the deblurring process under both generative and classical priors.

Invertible generative models for inverse problems: mitigating representation error and dataset bias

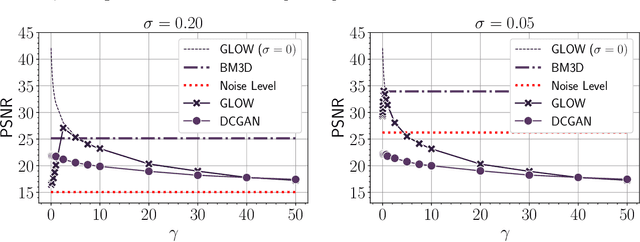
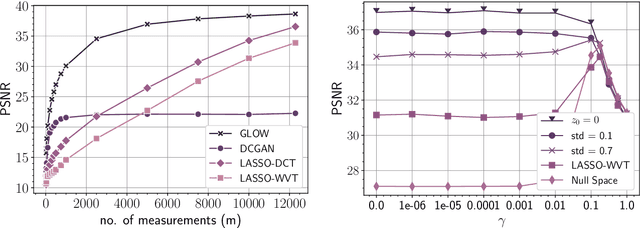
Trained generative models have shown remarkable performance as priors for inverse problems in imaging. For example, Generative Adversarial Network priors permit recovery of test images from 5-10x fewer measurements than sparsity priors. Unfortunately, these models may be unable to represent any particular image because of architectural choices, mode collapse, and bias in the training dataset. In this paper, we demonstrate that invertible neural networks, which have zero representation error by design, can be effective natural signal priors at inverse problems such as denoising, compressive sensing, and inpainting. Given a trained generative model, we study the empirical risk formulation of the desired inverse problem under a regularization that promotes high likelihood images, either directly by penalization or algorithmically by initialization. For compressive sensing, invertible priors can yield higher accuracy than sparsity priors across almost all undersampling ratios. For the same accuracy on test images, they can use 10-20x fewer measurements. We demonstrate that invertible priors can yield better reconstructions than sparsity priors for images that have rare features of variation within the biased training set, including out-of-distribution natural images.

Deep Ptych: Subsampled Fourier Ptychography using Generative Priors

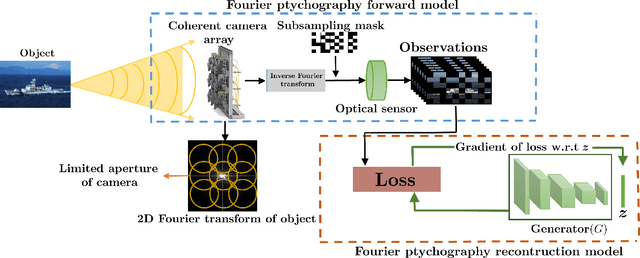
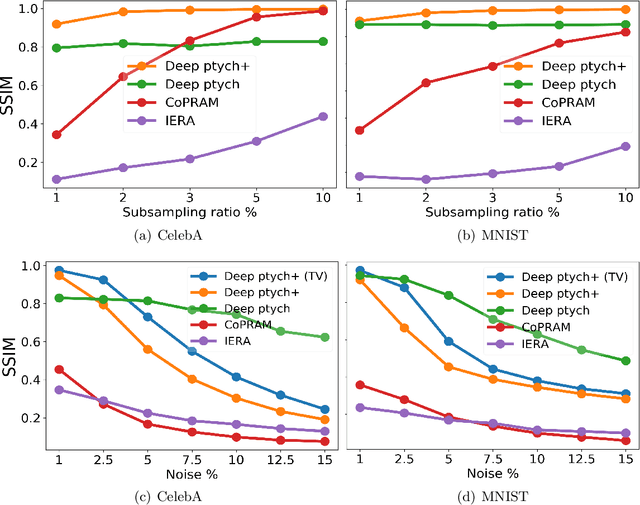
This paper proposes a novel framework to regularize the highly ill-posed and non-linear Fourier ptychography problem using generative models. We demonstrate experimentally that our proposed algorithm, Deep Ptych, outperforms the existing Fourier ptychography techniques, in terms of quality of reconstruction and robustness against noise, using far fewer samples. We further modify the proposed approach to allow the generative model to explore solutions outside the range, leading to improved performance.

Leveraging Deep Stein's Unbiased Risk Estimator for Unsupervised X-ray Denoising

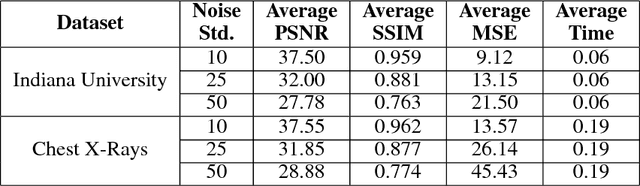
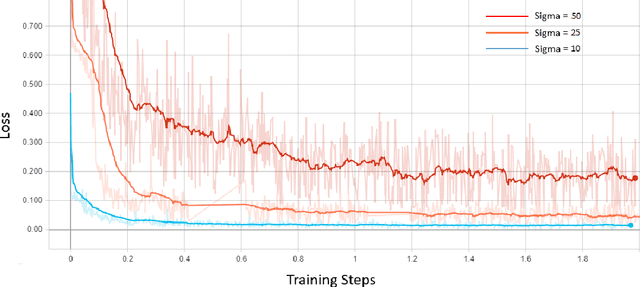
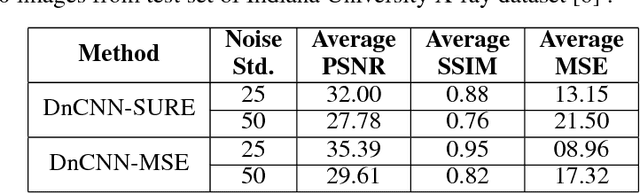
Among the plethora of techniques devised to curb the prevalence of noise in medical images, deep learning based approaches have shown the most promise. However, one critical limitation of these deep learning based denoisers is the requirement of high-quality noiseless ground truth images that are difficult to obtain in many medical imaging applications such as X-rays. To circumvent this issue, we leverage recently proposed approach of [7] that incorporates Stein's Unbiased Risk Estimator (SURE) to train a deep convolutional neural network without requiring denoised ground truth X-ray data. Our experimental results demonstrate the effectiveness of SURE based approach for denoising X-ray images.

Robust Compressive Phase Retrieval via Deep Generative Priors

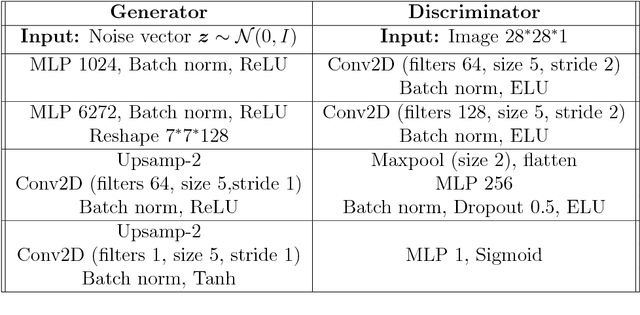
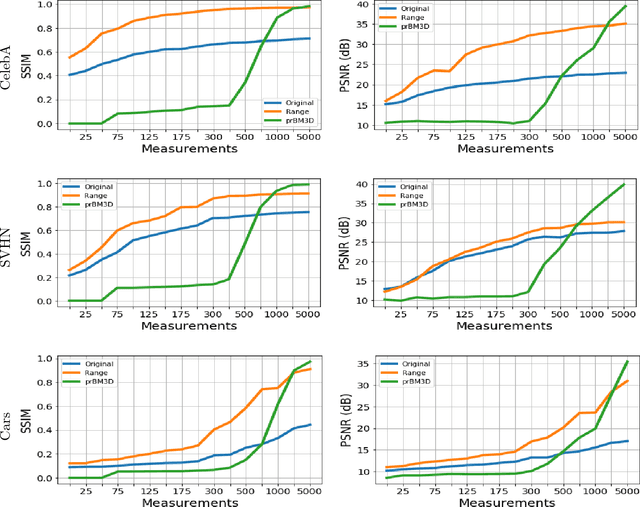
This paper proposes a new framework to regularize the highly ill-posed and non-linear phase retrieval problem through deep generative priors using simple gradient descent algorithm. We experimentally show effectiveness of proposed algorithm for random Gaussian measurements (practically relevant in imaging through scattering media) and Fourier friendly measurements (relevant in optical set ups). We demonstrate that proposed approach achieves impressive results when compared with traditional hand engineered priors including sparsity and denoising frameworks for number of measurements and robustness against noise. Finally, we show the effectiveness of the proposed approach on a real transmission matrix dataset in an actual application of multiple scattering media imaging.

Blind Image Deconvolution using Deep Generative Priors

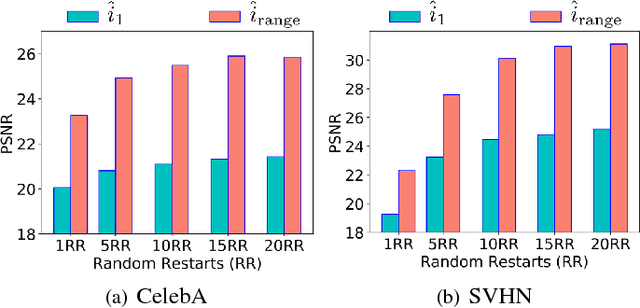
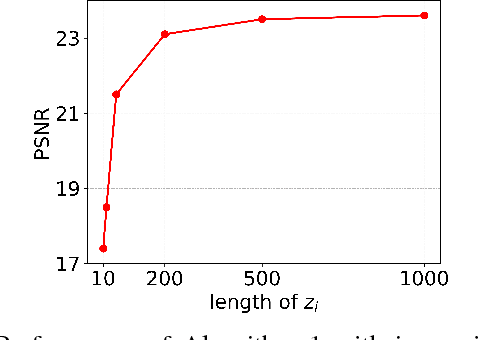
This paper proposes a new framework to regularize the \textit{ill-posed} and \textit{non-linear} blind image deconvolution problem by using deep generative priors. We employ two separate deep generative models --- one trained to produce sharp images while the other trained to generate blur kernels from lower-dimensional parameters. The regularized problem is efficiently solved by simple alternating gradient descent algorithm operating in the latent lower-dimensional space of each generative model. We empirically show that by doing so, excellent image deblurring results are achieved even under extravagantly large blurs, and heavy noise. Our proposed method is in stark contrast to the conventional end-to-end approaches, where a deep neural network is trained on blurred input, and the corresponding sharp output images while completely ignoring the knowledge of the underlying forward map (convolution operator) in image blurring.