Class-Specific Blind Deconvolutional Phase Retrieval Under a Generative Prior
Paper and Code
Feb 28, 2020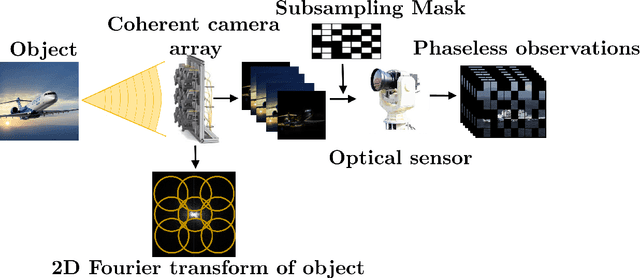
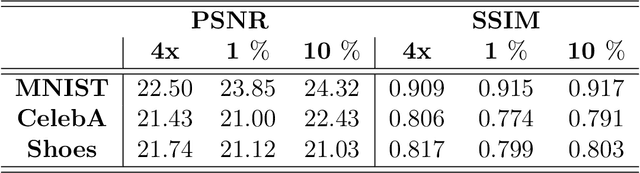


In this paper, we consider the highly ill-posed problem of jointly recovering two real-valued signals from the phaseless measurements of their circular convolution. The problem arises in various imaging modalities such as Fourier ptychography, X-ray crystallography, and in visible light communication. We propose to solve this inverse problem using alternating gradient descent algorithm under two pretrained deep generative networks as priors; one is trained on sharp images and the other on blur kernels. The proposed recovery algorithm strives to find a sharp image and a blur kernel in the range of the respective pre-generators that \textit{best} explain the forward measurement model. In doing so, we are able to reconstruct quality image estimates. Moreover, the numerics show that the proposed approach performs well on the challenging measurement models that reflect the physically realizable imaging systems and is also robust to noise
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge