Neural Network Pruning Through Constrained Reinforcement Learning

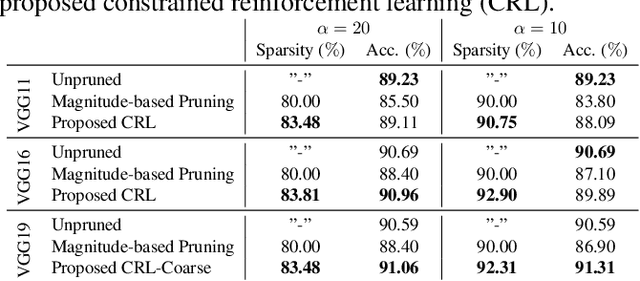
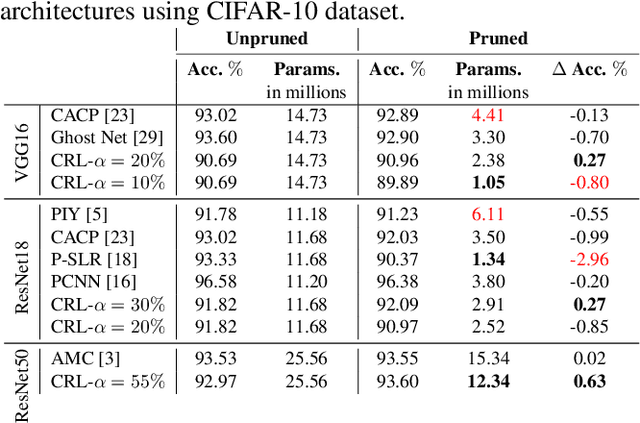
Network pruning reduces the size of neural networks by removing (pruning) neurons such that the performance drop is minimal. Traditional pruning approaches focus on designing metrics to quantify the usefulness of a neuron which is often quite tedious and sub-optimal. More recent approaches have instead focused on training auxiliary networks to automatically learn how useful each neuron is however, they often do not take computational limitations into account. In this work, we propose a general methodology for pruning neural networks. Our proposed methodology can prune neural networks to respect pre-defined computational budgets on arbitrary, possibly non-differentiable, functions. Furthermore, we only assume the ability to be able to evaluate these functions for different inputs, and hence they do not need to be fully specified beforehand. We achieve this by proposing a novel pruning strategy via constrained reinforcement learning algorithms. We prove the effectiveness of our approach via comparison with state-of-the-art methods on standard image classification datasets. Specifically, we reduce 83-92.90 of total parameters on various variants of VGG while achieving comparable or better performance than that of original networks. We also achieved 75.09 reduction in parameters on ResNet18 without incurring any loss in accuracy.

Inverse Constrained Reinforcement Learning

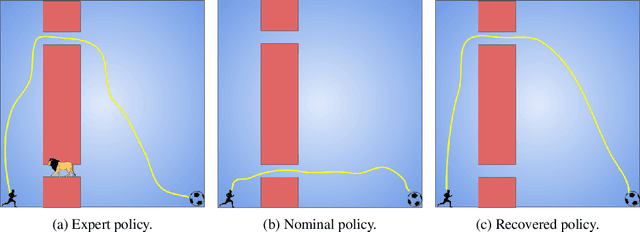
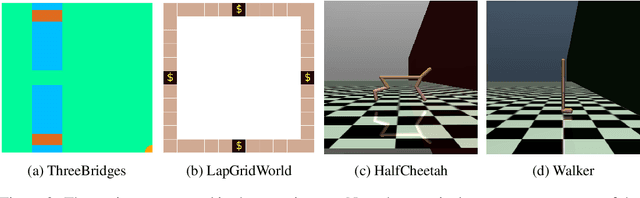
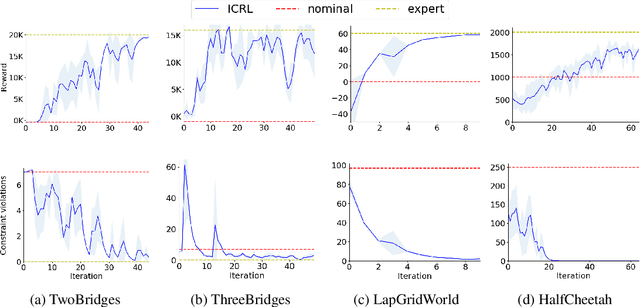
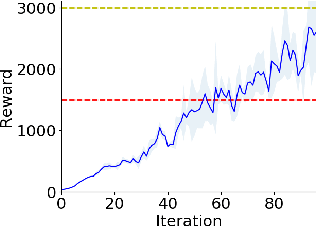
Standard reinforcement learning (RL) algorithms train agents to maximize given reward functions. However, many real-world applications of RL require agents to also satisfy certain constraints which may, for example, be motivated by safety concerns. Constrained RL algorithms approach this problem by training agents to maximize given reward functions while respecting \textit{explicitly} defined constraints. However, in many cases, manually designing accurate constraints is a challenging task. In this work, given a reward function and a set of demonstrations from an expert that maximizes this reward function while respecting \textit{unknown} constraints, we propose a framework to learn the most likely constraints that the expert respects. We then train agents to maximize the given reward function subject to the learned constraints. Previous works in this regard have either mainly been restricted to tabular settings or specific types of constraints or assume knowledge of transition dynamics of the environment. In contrast, we empirically show that our framework is able to learn arbitrary \textit{Markovian} constraints in high-dimensions in a model-free setting.

Learning To Solve Differential Equations Across Initial Conditions

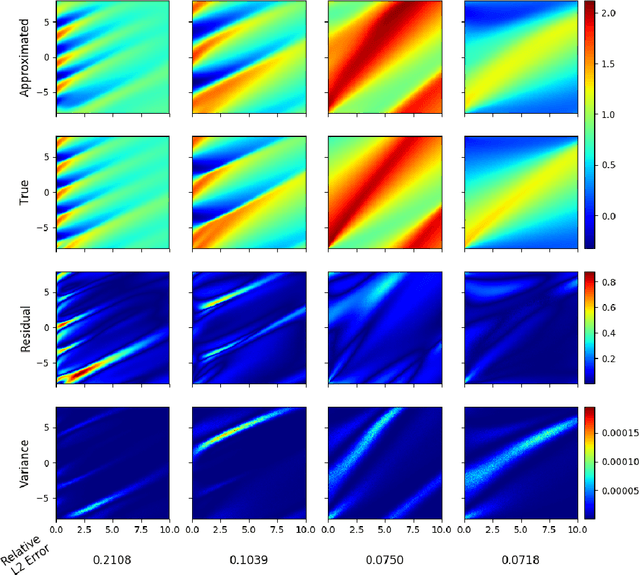
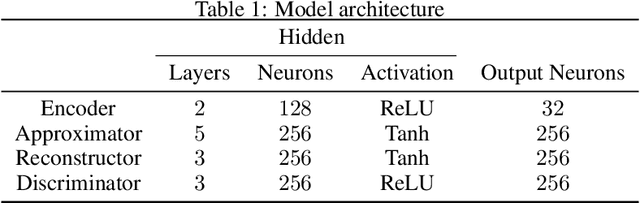
Recently, there has been a lot of interest in using neural networks for solving partial differential equations. A number of neural network-based partial differential equation solvers have been formulated which provide performances equivalent, and in some cases even superior, to classical solvers. However, these neural solvers, in general, need to be retrained each time the initial conditions or the domain of the partial differential equation changes. In this work, we posit the problem of approximating the solution of a fixed partial differential equation for any arbitrary initial conditions as learning a conditional probability distribution. We demonstrate the utility of our method on Burger's Equation.