Alessandra Sutti
Accelerating Experimental Design by Incorporating Experimenter Hunches
Jul 22, 2019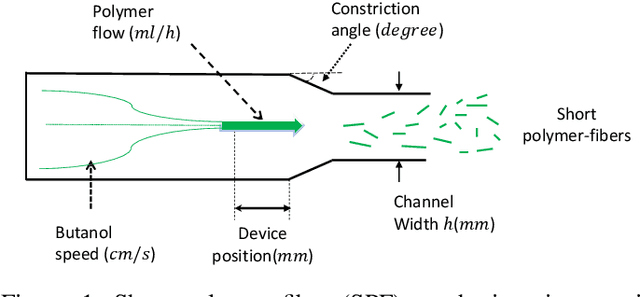
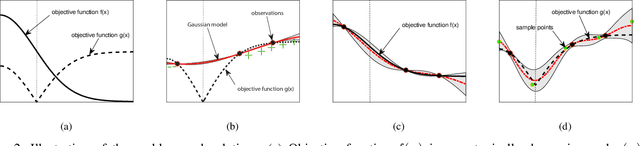
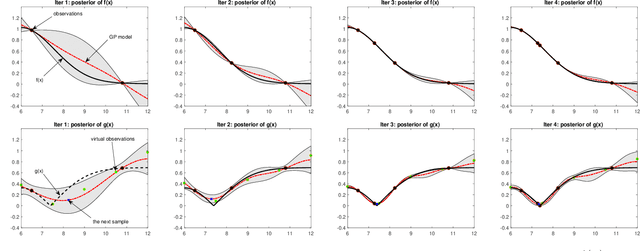
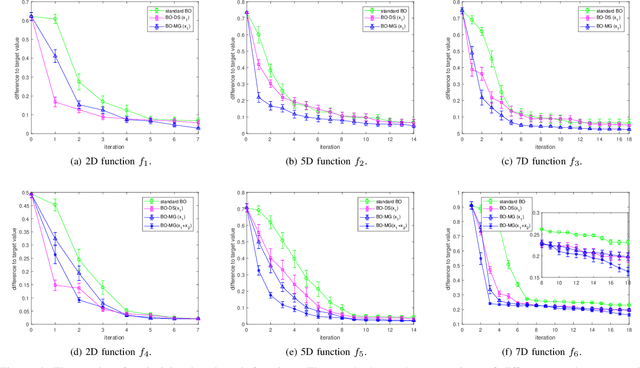
Abstract:Experimental design is a process of obtaining a product with target property via experimentation. Bayesian optimization offers a sample-efficient tool for experimental design when experiments are expensive. Often, expert experimenters have 'hunches' about the behavior of the experimental system, offering potentials to further improve the efficiency. In this paper, we consider per-variable monotonic trend in the underlying property that results in a unimodal trend in those variables for a target value optimization. For example, sweetness of a candy is monotonic to the sugar content. However, to obtain a target sweetness, the utility of the sugar content becomes a unimodal function, which peaks at the value giving the target sweetness and falls off both ways. In this paper, we propose a novel method to solve such problems that achieves two main objectives: a) the monotonicity information is used to the fullest extent possible, whilst ensuring that b) the convergence guarantee remains intact. This is achieved by a two-stage Gaussian process modeling, where the first stage uses the monotonicity trend to model the underlying property, and the second stage uses `virtual' samples, sampled from the first, to model the target value optimization function. The process is made theoretically consistent by adding appropriate adjustment factor in the posterior computation, necessitated because of using the `virtual' samples. The proposed method is evaluated through both simulations and real world experimental design problems of a) new short polymer fiber with the target length, and b) designing of a new three dimensional porous scaffolding with a target porosity. In all scenarios our method demonstrates faster convergence than the basic Bayesian optimization approach not using such `hunches'.
Bayesian functional optimisation with shape prior
Sep 19, 2018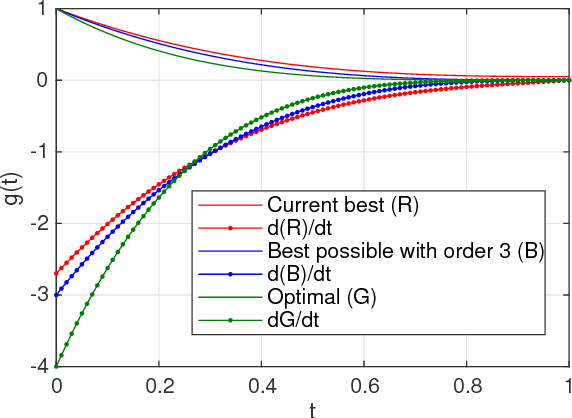

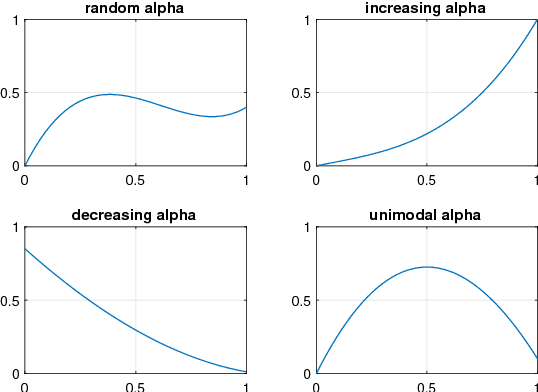
Abstract:Real world experiments are expensive, and thus it is important to reach a target in minimum number of experiments. Experimental processes often involve control variables that changes over time. Such problems can be formulated as a functional optimisation problem. We develop a novel Bayesian optimisation framework for such functional optimisation of expensive black-box processes. We represent the control function using Bernstein polynomial basis and optimise in the coefficient space. We derive the theory and practice required to dynamically adjust the order of the polynomial degree, and show how prior information about shape can be integrated. We demonstrate the effectiveness of our approach for short polymer fibre design and optimising learning rate schedules for deep networks.
Kernel Pre-Training in Feature Space via m-Kernels
May 21, 2018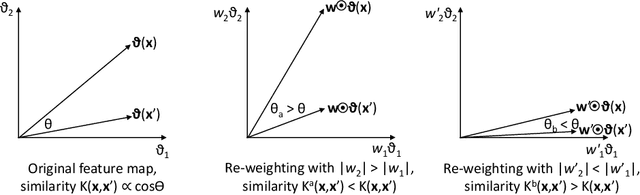


Abstract:This paper presents a novel approach to kernel tuning. The method presented borrows techniques from reproducing kernel Banach space (RKBS) theory and tensor kernels and leverages them to convert (re-weight in feature space) existing kernel functions into new, problem-specific kernels using auxiliary data. The proposed method is applied to accelerating Bayesian optimisation via covariance (kernel) function pre-tuning for short-polymer fibre manufacture and alloy design.
Covariance Function Pre-Training with m-Kernels for Accelerated Bayesian Optimisation
Mar 13, 2018
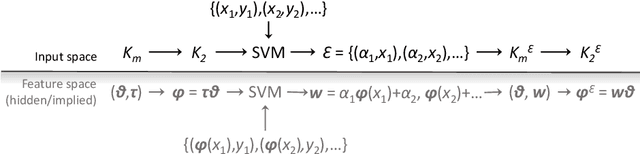
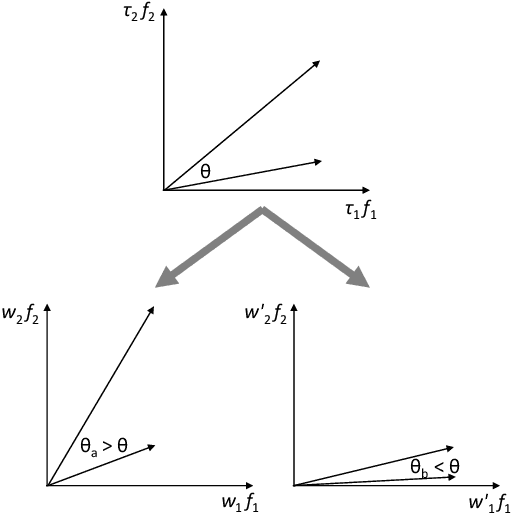
Abstract:The paper presents a novel approach to direct covariance function learning for Bayesian optimisation, with particular emphasis on experimental design problems where an existing corpus of condensed knowledge is present. The method presented borrows techniques from reproducing kernel Banach space theory (specifically m-kernels) and leverages them to convert (or re-weight) existing covariance functions into new, problem-specific covariance functions. The key advantage of this approach is that rather than relying on the user to manually select (with some hyperparameter tuning and experimentation) an appropriate covariance function it constructs the covariance function to specifically match the problem at hand. The technique is demonstrated on two real-world problems - specifically alloy design and short-polymer fibre manufacturing - as well as a selected test function.
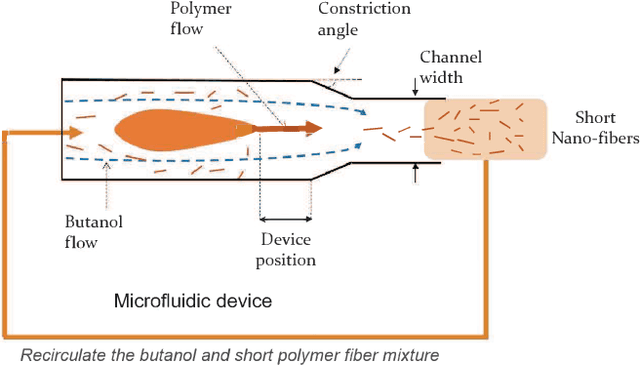
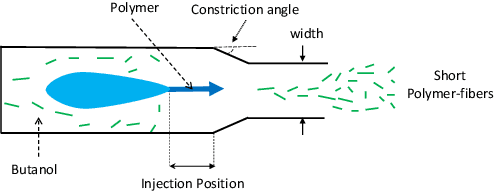
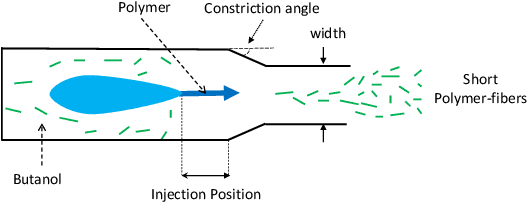
Rapid Bayesian optimisation for synthesis of short polymer fiber materials
Feb 16, 2018

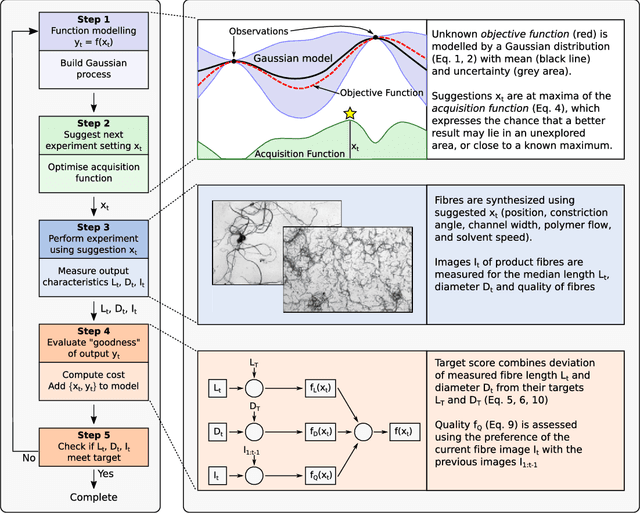

Abstract:The discovery of processes for the synthesis of new materials involves many decisions about process design, operation, and material properties. Experimentation is crucial but as complexity increases, exploration of variables can become impractical using traditional combinatorial approaches. We describe an iterative method which uses machine learning to optimise process development, incorporating multiple qualitative and quantitative objectives. We demonstrate the method with a novel fluid processing platform for synthesis of short polymer fibers, and show how the synthesis process can be efficiently directed to achieve material and process objectives.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge