Bayesian functional optimisation with shape prior
Paper and Code
Sep 19, 2018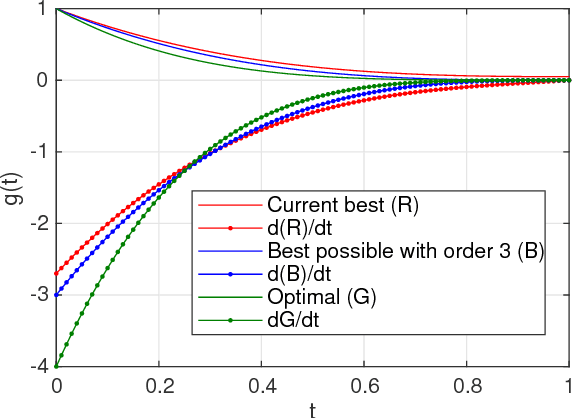

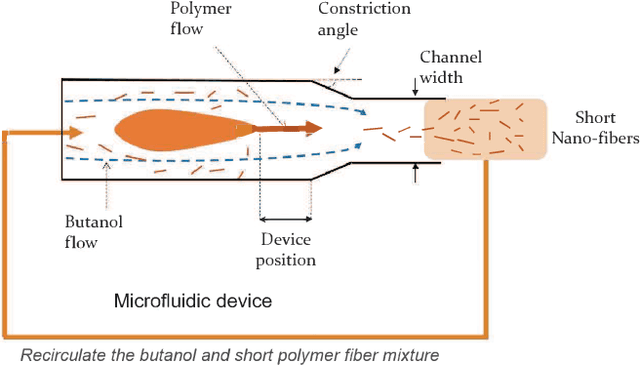
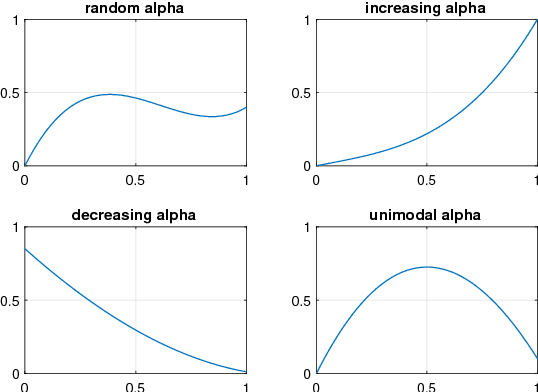
Real world experiments are expensive, and thus it is important to reach a target in minimum number of experiments. Experimental processes often involve control variables that changes over time. Such problems can be formulated as a functional optimisation problem. We develop a novel Bayesian optimisation framework for such functional optimisation of expensive black-box processes. We represent the control function using Bernstein polynomial basis and optimise in the coefficient space. We derive the theory and practice required to dynamically adjust the order of the polynomial degree, and show how prior information about shape can be integrated. We demonstrate the effectiveness of our approach for short polymer fibre design and optimising learning rate schedules for deep networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge