Bayesian functional optimisation with shape prior

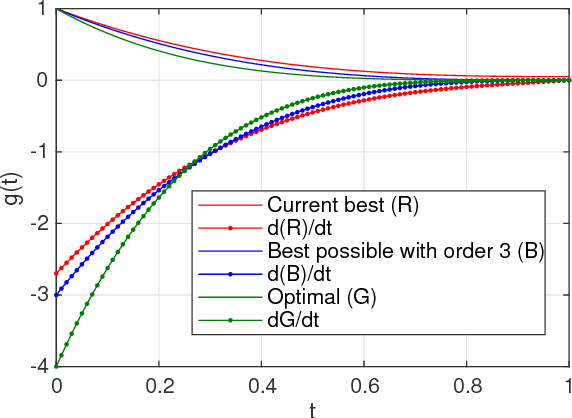
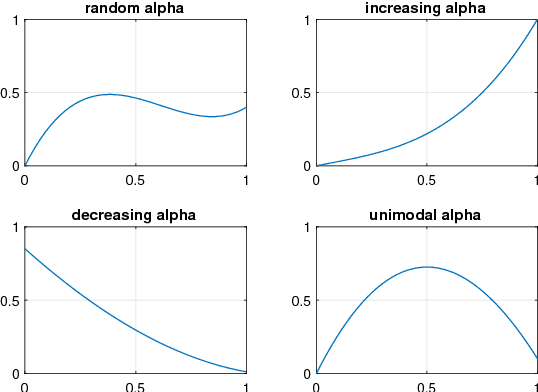
Real world experiments are expensive, and thus it is important to reach a target in minimum number of experiments. Experimental processes often involve control variables that changes over time. Such problems can be formulated as a functional optimisation problem. We develop a novel Bayesian optimisation framework for such functional optimisation of expensive black-box processes. We represent the control function using Bernstein polynomial basis and optimise in the coefficient space. We derive the theory and practice required to dynamically adjust the order of the polynomial degree, and show how prior information about shape can be integrated. We demonstrate the effectiveness of our approach for short polymer fibre design and optimising learning rate schedules for deep networks.

Rapid Bayesian optimisation for synthesis of short polymer fiber materials

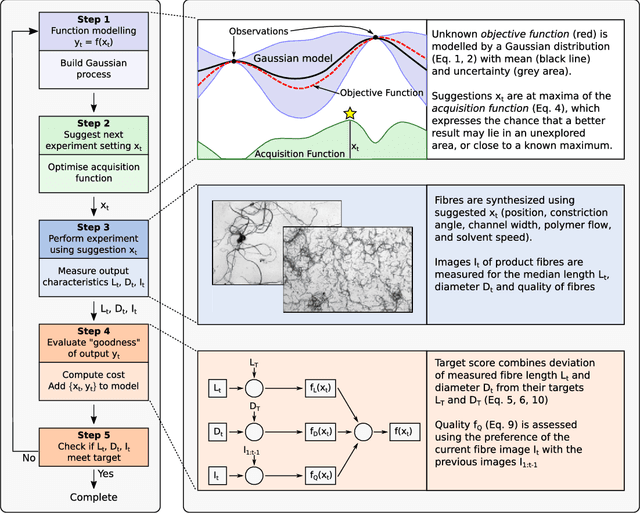
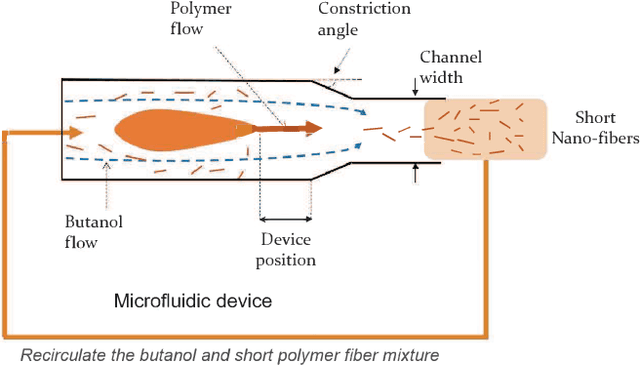
The discovery of processes for the synthesis of new materials involves many decisions about process design, operation, and material properties. Experimentation is crucial but as complexity increases, exploration of variables can become impractical using traditional combinatorial approaches. We describe an iterative method which uses machine learning to optimise process development, incorporating multiple qualitative and quantitative objectives. We demonstrate the method with a novel fluid processing platform for synthesis of short polymer fibers, and show how the synthesis process can be efficiently directed to achieve material and process objectives.