Novel Kernel Models and Exact Representor Theory for Neural Networks Beyond the Over-Parameterized Regime

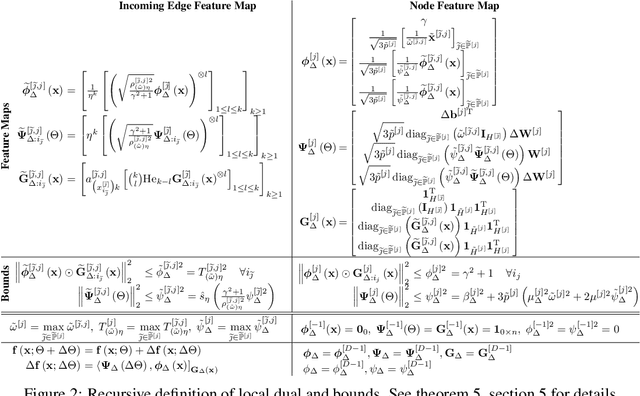
This paper presents two models of neural-networks and their training applicable to neural networks of arbitrary width, depth and topology, assuming only finite-energy neural activations; and a novel representor theory for neural networks in terms of a matrix-valued kernel. The first model is exact (un-approximated) and global, casting the neural network as an elements in a reproducing kernel Banach space (RKBS); we use this model to provide tight bounds on Rademacher complexity. The second model is exact and local, casting the change in neural network function resulting from a bounded change in weights and biases (ie. a training step) in reproducing kernel Hilbert space (RKHS) in terms of a local-intrinsic neural kernel (LiNK). This local model provides insight into model adaptation through tight bounds on Rademacher complexity of network adaptation. We also prove that the neural tangent kernel (NTK) is a first-order approximation of the LiNK kernel. Finally, and noting that the LiNK does not provide a representor theory for technical reasons, we present an exact novel representor theory for layer-wise neural network training with unregularized gradient descent in terms of a local-extrinsic neural kernel (LeNK). This representor theory gives insight into the role of higher-order statistics in neural network training and the effect of kernel evolution in neural-network kernel models. Throughout the paper (a) feedforward ReLU networks and (b) residual networks (ResNet) are used as illustrative examples.

Enhanced Bayesian Optimization via Preferential Modeling of Abstract Properties

Experimental (design) optimization is a key driver in designing and discovering new products and processes. Bayesian Optimization (BO) is an effective tool for optimizing expensive and black-box experimental design processes. While Bayesian optimization is a principled data-driven approach to experimental optimization, it learns everything from scratch and could greatly benefit from the expertise of its human (domain) experts who often reason about systems at different abstraction levels using physical properties that are not necessarily directly measured (or measurable). In this paper, we propose a human-AI collaborative Bayesian framework to incorporate expert preferences about unmeasured abstract properties into the surrogate modeling to further boost the performance of BO. We provide an efficient strategy that can also handle any incorrect/misleading expert bias in preferential judgments. We discuss the convergence behavior of our proposed framework. Our experimental results involving synthetic functions and real-world datasets show the superiority of our method against the baselines.

PINN-BO: A Black-box Optimization Algorithm using Physics-Informed Neural Networks

Black-box optimization is a powerful approach for discovering global optima in noisy and expensive black-box functions, a problem widely encountered in real-world scenarios. Recently, there has been a growing interest in leveraging domain knowledge to enhance the efficacy of machine learning methods. Partial Differential Equations (PDEs) often provide an effective means for elucidating the fundamental principles governing the black-box functions. In this paper, we propose PINN-BO, a black-box optimization algorithm employing Physics-Informed Neural Networks that integrates the knowledge from Partial Differential Equations (PDEs) to improve the sample efficiency of the optimization. We analyze the theoretical behavior of our algorithm in terms of regret bound using advances in NTK theory and prove that the use of the PDE alongside the black-box function evaluations, PINN-BO leads to a tighter regret bound. We perform several experiments on a variety of optimization tasks and show that our algorithm is more sample-efficient compared to existing methods.

BO-Muse: A human expert and AI teaming framework for accelerated experimental design

In this paper we introduce BO-Muse, a new approach to human-AI teaming for the optimization of expensive black-box functions. Inspired by the intrinsic difficulty of extracting expert knowledge and distilling it back into AI models and by observations of human behaviour in real-world experimental design, our algorithm lets the human expert take the lead in the experimental process. The human expert can use their domain expertise to its full potential, while the AI plays the role of a muse, injecting novelty and searching for areas of weakness to break the human out of over-exploitation induced by cognitive entrenchment. With mild assumptions, we show that our algorithm converges sub-linearly, at a rate faster than the AI or human alone. We validate our algorithm using synthetic data and with human experts performing real-world experiments.

Gradient Descent in Neural Networks as Sequential Learning in RKBS

The study of Neural Tangent Kernels (NTKs) has provided much needed insight into convergence and generalization properties of neural networks in the over-parametrized (wide) limit by approximating the network using a first-order Taylor expansion with respect to its weights in the neighborhood of their initialization values. This allows neural network training to be analyzed from the perspective of reproducing kernel Hilbert spaces (RKHS), which is informative in the over-parametrized regime, but a poor approximation for narrower networks as the weights change more during training. Our goal is to extend beyond the limits of NTK toward a more general theory. We construct an exact power-series representation of the neural network in a finite neighborhood of the initial weights as an inner product of two feature maps, respectively from data and weight-step space, to feature space, allowing neural network training to be analyzed from the perspective of reproducing kernel {\em Banach} space (RKBS). We prove that, regardless of width, the training sequence produced by gradient descent can be exactly replicated by regularized sequential learning in RKBS. Using this, we present novel bound on uniform convergence where the iterations count and learning rate play a central role, giving new theoretical insight into neural network training.

Sequential Subspace Search for Functional Bayesian Optimization Incorporating Experimenter Intuition

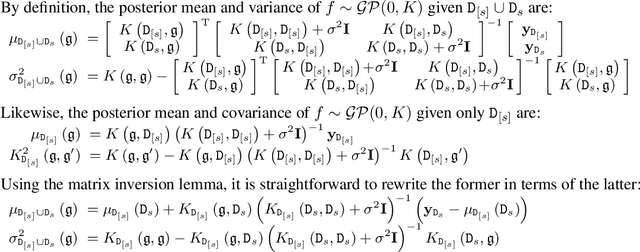
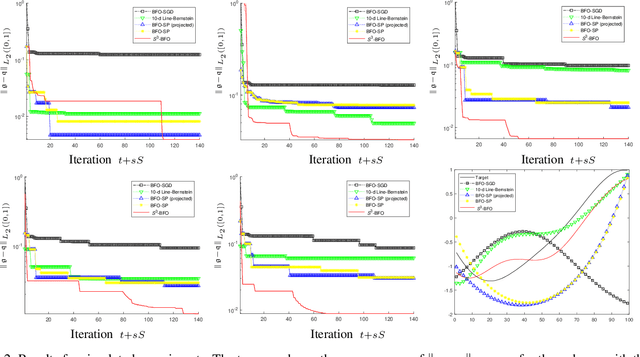
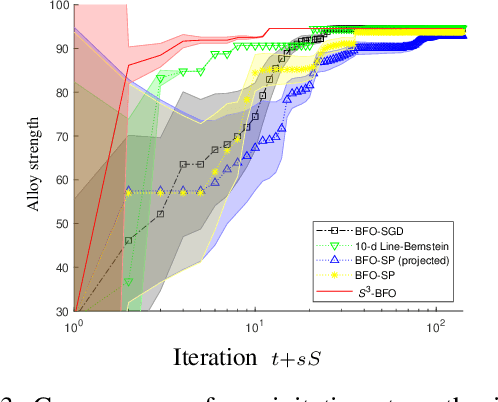
We propose an algorithm for Bayesian functional optimisation - that is, finding the function to optimise a process - guided by experimenter beliefs and intuitions regarding the expected characteristics (length-scale, smoothness, cyclicity etc.) of the optimal solution encoded into the covariance function of a Gaussian Process. Our algorithm generates a sequence of finite-dimensional random subspaces of functional space spanned by a set of draws from the experimenter's Gaussian Process. Standard Bayesian optimisation is applied on each subspace, and the best solution found used as a starting point (origin) for the next subspace. Using the concept of effective dimensionality, we analyse the convergence of our algorithm and provide a regret bound to show that our algorithm converges in sub-linear time provided a finite effective dimension exists. We test our algorithm in simulated and real-world experiments, namely blind function matching, finding the optimal precipitation-strengthening function for an aluminium alloy, and learning rate schedule optimisation for deep networks.

From deep to Shallow: Equivalent Forms of Deep Networks in Reproducing Kernel Krein Space and Indefinite Support Vector Machines

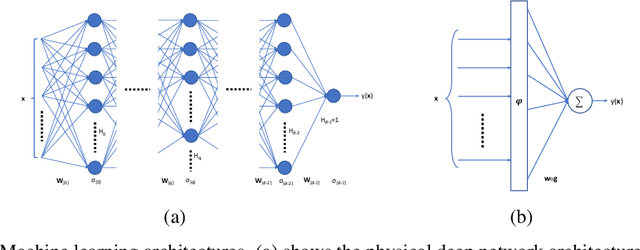
In this paper we explore a connection between deep networks and learning in reproducing kernel Krein space. Our approach is based on the concept of push-forward - that is, taking a fixed non-linear transform on a linear projection and converting it to a linear projection on the output of a fixed non-linear transform, aka pushing the weights forward through the non-linearity. Applying this repeatedly from the input to the output of a deep network, the weights can be progressively "pushed" to the output layer, resulting in a flat network that has the form of a fixed non-linear map (whose form is determined by the structure of the deep network) followed by a linear projection determined by the weight matrices - that is, we take a deep network and convert it to an equivalent (indefinite) support vector machine. We then investigate the implications of this transformation for capacity control and generalisation, and provide a bound on generalisation error in the deep network in terms of generalisation error in reproducing kernel Krein space.

Bayesian Optimization for Categorical and Category-Specific Continuous Inputs

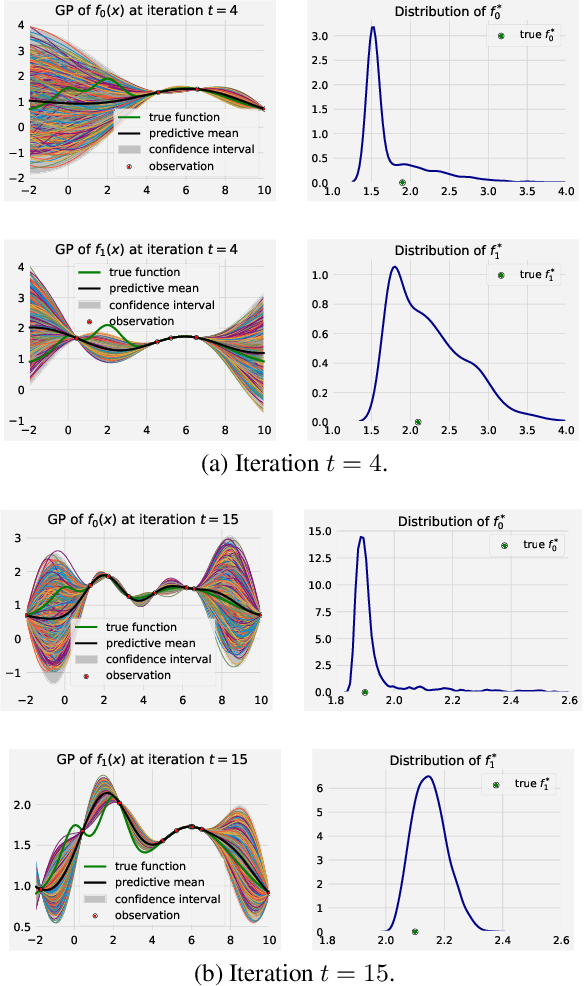
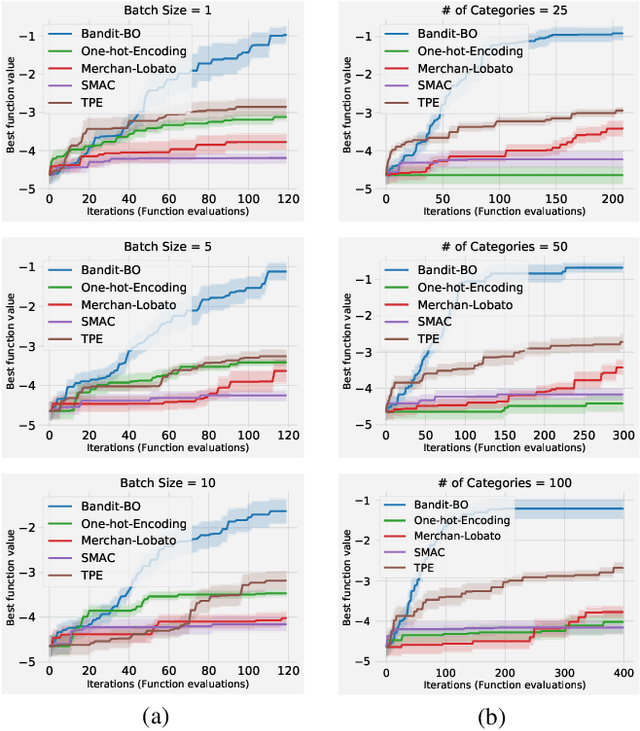
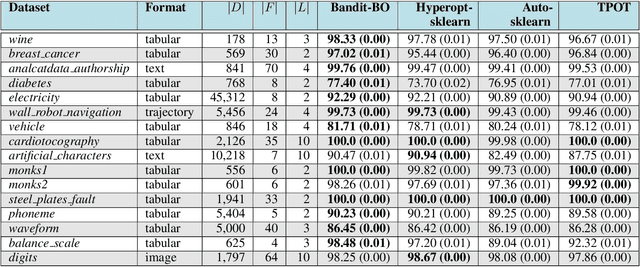
Many real-world functions are defined over both categorical and category-specific continuous variables and thus cannot be optimized by traditional Bayesian optimization (BO) methods. To optimize such functions, we propose a new method that formulates the problem as a multi-armed bandit problem, wherein each category corresponds to an arm with its reward distribution centered around the optimum of the objective function in continuous variables. Our goal is to identify the best arm and the maximizer of the corresponding continuous function simultaneously. Our algorithm uses a Thompson sampling scheme that helps connecting both multi-arm bandit and BO in a unified framework. We extend our method to batch BO to allow parallel optimization when multiple resources are available. We theoretically analyze our method for convergence and prove sub-linear regret bounds. We perform a variety of experiments: optimization of several benchmark functions, hyper-parameter tuning of a neural network, and automatic selection of the best machine learning model along with its optimal hyper-parameters (a.k.a automated machine learning). Comparisons with other methods demonstrate the effectiveness of our proposed method.

Cost-aware Multi-objective Bayesian optimisation

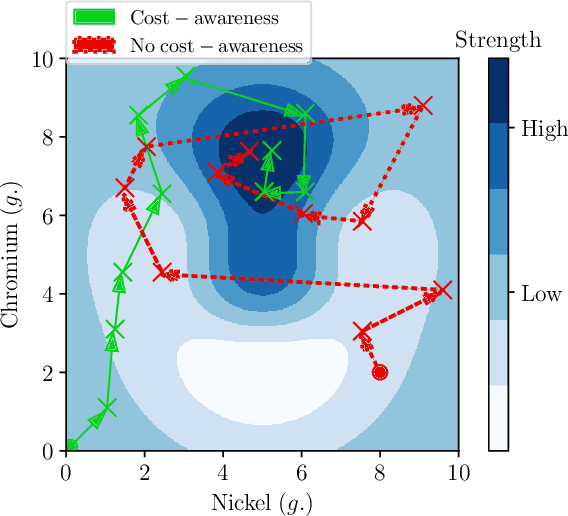
The notion of expense in Bayesian optimisation generally refers to the uniformly expensive cost of function evaluations over the whole search space. However, in some scenarios, the cost of evaluation for black-box objective functions is non-uniform since different inputs from search space may incur different costs for function evaluations. We introduce a cost-aware multi-objective Bayesian optimisation with non-uniform evaluation cost over objective functions by defining cost-aware constraints over the search space. The cost-aware constraints are a sorted tuple of indexes that demonstrate the ordering of dimensions of the search space based on the user's prior knowledge about their cost of usage. We formulate a new multi-objective Bayesian optimisation acquisition function with detailed analysis of the convergence that incorporates this cost-aware constraints while optimising the objective functions. We demonstrate our algorithm based on synthetic and real-world problems in hyperparameter tuning of neural networks and random forests.

Stable Bayesian Optimisation via Direct Stability Quantification

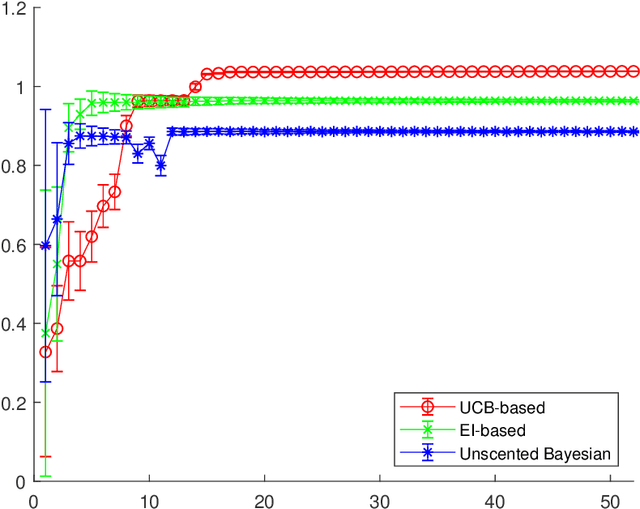
In this paper we consider the problem of finding stable maxima of expensive (to evaluate) functions. We are motivated by the optimisation of physical and industrial processes where, for some input ranges, small and unavoidable variations in inputs lead to unacceptably large variation in outputs. Our approach uses multiple gradient Gaussian Process models to estimate the probability that worst-case output variation for specified input perturbation exceeded the desired maxima, and these probabilities are then used to (a) guide the optimisation process toward solutions satisfying our stability criteria and (b) post-filter results to find the best stable solution. We exhibit our algorithm on synthetic and real-world problems and demonstrate that it is able to effectively find stable maxima.