Novel Kernel Models and Exact Representor Theory for Neural Networks Beyond the Over-Parameterized Regime
Paper and Code
May 24, 2024
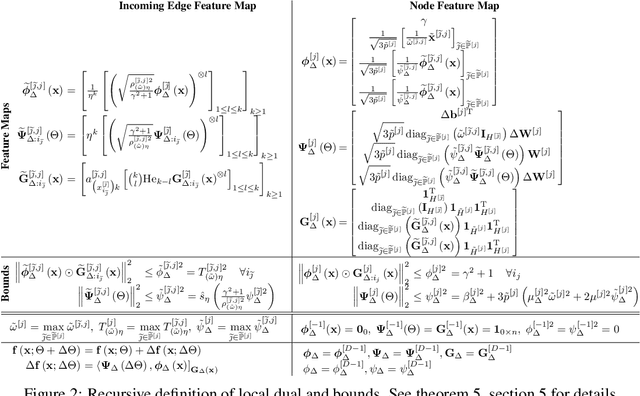
This paper presents two models of neural-networks and their training applicable to neural networks of arbitrary width, depth and topology, assuming only finite-energy neural activations; and a novel representor theory for neural networks in terms of a matrix-valued kernel. The first model is exact (un-approximated) and global, casting the neural network as an elements in a reproducing kernel Banach space (RKBS); we use this model to provide tight bounds on Rademacher complexity. The second model is exact and local, casting the change in neural network function resulting from a bounded change in weights and biases (ie. a training step) in reproducing kernel Hilbert space (RKHS) in terms of a local-intrinsic neural kernel (LiNK). This local model provides insight into model adaptation through tight bounds on Rademacher complexity of network adaptation. We also prove that the neural tangent kernel (NTK) is a first-order approximation of the LiNK kernel. Finally, and noting that the LiNK does not provide a representor theory for technical reasons, we present an exact novel representor theory for layer-wise neural network training with unregularized gradient descent in terms of a local-extrinsic neural kernel (LeNK). This representor theory gives insight into the role of higher-order statistics in neural network training and the effect of kernel evolution in neural-network kernel models. Throughout the paper (a) feedforward ReLU networks and (b) residual networks (ResNet) are used as illustrative examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge