Thomas Dorin
Kernel Pre-Training in Feature Space via m-Kernels
May 21, 2018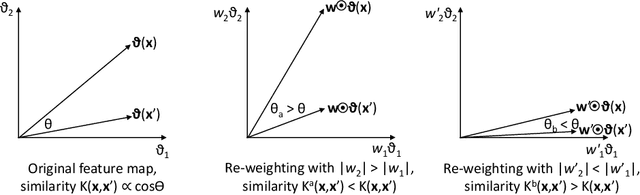


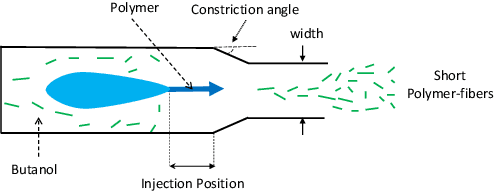
Abstract:This paper presents a novel approach to kernel tuning. The method presented borrows techniques from reproducing kernel Banach space (RKBS) theory and tensor kernels and leverages them to convert (re-weight in feature space) existing kernel functions into new, problem-specific kernels using auxiliary data. The proposed method is applied to accelerating Bayesian optimisation via covariance (kernel) function pre-tuning for short-polymer fibre manufacture and alloy design.
Covariance Function Pre-Training with m-Kernels for Accelerated Bayesian Optimisation
Mar 13, 2018
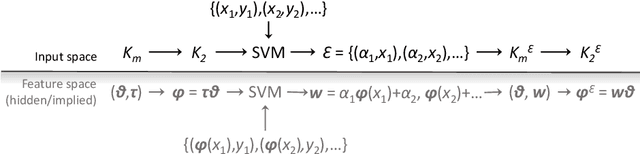
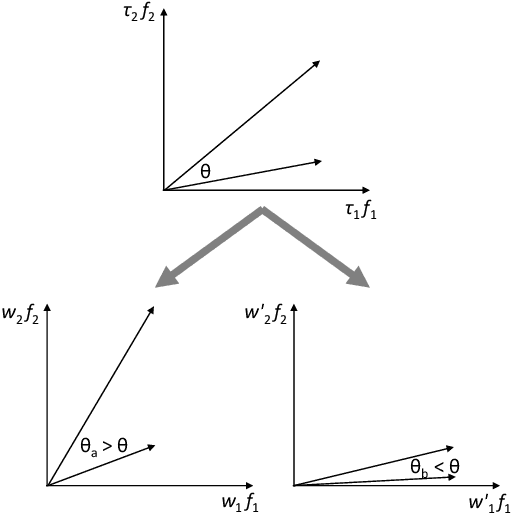
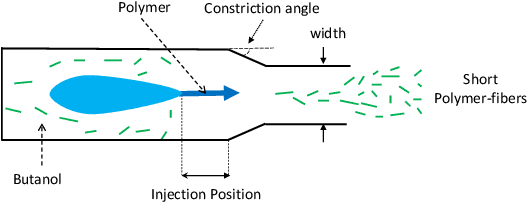
Abstract:The paper presents a novel approach to direct covariance function learning for Bayesian optimisation, with particular emphasis on experimental design problems where an existing corpus of condensed knowledge is present. The method presented borrows techniques from reproducing kernel Banach space theory (specifically m-kernels) and leverages them to convert (or re-weight) existing covariance functions into new, problem-specific covariance functions. The key advantage of this approach is that rather than relying on the user to manually select (with some hyperparameter tuning and experimentation) an appropriate covariance function it constructs the covariance function to specifically match the problem at hand. The technique is demonstrated on two real-world problems - specifically alloy design and short-polymer fibre manufacturing - as well as a selected test function.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge