A Granger-Causal Perspective on Gradient Descent with Application to Pruning

Stochastic Gradient Descent (SGD) is the main approach to optimizing neural networks. Several generalization properties of deep networks, such as convergence to a flatter minima, are believed to arise from SGD. This article explores the causality aspect of gradient descent. Specifically, we show that the gradient descent procedure has an implicit granger-causal relationship between the reduction in loss and a change in parameters. By suitable modifications, we make this causal relationship explicit. A causal approach to gradient descent has many significant applications which allow greater control. In this article, we illustrate the significance of the causal approach using the application of Pruning. The causal approach to pruning has several interesting properties - (i) We observe a phase shift as the percentage of pruned parameters increase. Such phase shift is indicative of an optimal pruning strategy. (ii) After pruning, we see that minima becomes "flatter", explaining the increase in accuracy after pruning weights.

Quantile Activation: departing from single point estimation for better generalization across distortions

A classifier is, in its essence, a function which takes an input and returns the class of the input and implicitly assumes an underlying distribution. We argue in this article that one has to move away from this basic tenet to obtain generalisation across distributions. Specifically, the class of the sample should depend on the points from its context distribution for better generalisation across distributions. How does one achieve this? The key idea is to adapt the outputs of each neuron of the network to its context distribution. We propose quantile activation, QACT, which, in simple terms, outputs the relative quantile of the sample in its context distribution, instead of the actual values in traditional networks. The scope of this article is to validate the proposed activation across several experimental settings, and compare it with conventional techniques. For this, we use the datasets developed to test robustness against distortions CIFAR10C, CIFAR100C, MNISTC, TinyImagenetC, and show that we achieve a significantly higher generalisation across distortions than the conventional classifiers, across different architectures. Although this paper is only a proof of concept, we surprisingly find that this approach outperforms DINOv2(small) at large distortions, even though DINOv2 is trained with a far bigger network on a considerably larger dataset.

A Novel Approach to Regularising 1NN classifier for Improved Generalization

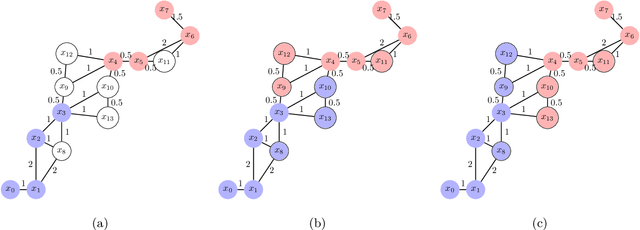
In this paper, we propose a class of non-parametric classifiers, that learn arbitrary boundaries and generalize well. Our approach is based on a novel way to regularize 1NN classifiers using a greedy approach. We refer to this class of classifiers as Watershed Classifiers. 1NN classifiers are known to trivially over-fit but have very large VC dimension, hence do not generalize well. We show that watershed classifiers can find arbitrary boundaries on any dense enough dataset, and, at the same time, have very small VC dimension; hence a watershed classifier leads to good generalization. Traditional approaches to regularize 1NN classifiers are to consider $K$ nearest neighbours. Neighbourhood component analysis (NCA) proposes a way to learn representations consistent with ($n-1$) nearest neighbour classifier, where $n$ denotes the size of the dataset. In this article, we propose a loss function which can learn representations consistent with watershed classifiers, and show that it outperforms the NCA baseline.

Decoupling Quantile Representations from Loss Functions

The simultaneous quantile regression (SQR) technique has been used to estimate uncertainties for deep learning models, but its application is limited by the requirement that the solution at the median quantile ({\tau} = 0.5) must minimize the mean absolute error (MAE). In this article, we address this limitation by demonstrating a duality between quantiles and estimated probabilities in the case of simultaneous binary quantile regression (SBQR). This allows us to decouple the construction of quantile representations from the loss function, enabling us to assign an arbitrary classifier f(x) at the median quantile and generate the full spectrum of SBQR quantile representations at different {\tau} values. We validate our approach through two applications: (i) detecting out-of-distribution samples, where we show that quantile representations outperform standard probability outputs, and (ii) calibrating models, where we demonstrate the robustness of quantile representations to distortions. We conclude with a discussion of several hypotheses arising from these findings.

A Robust Morphological Approach for Semantic Segmentation of Very High Resolution Images

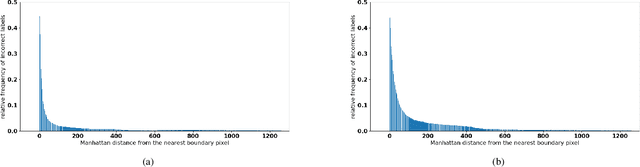
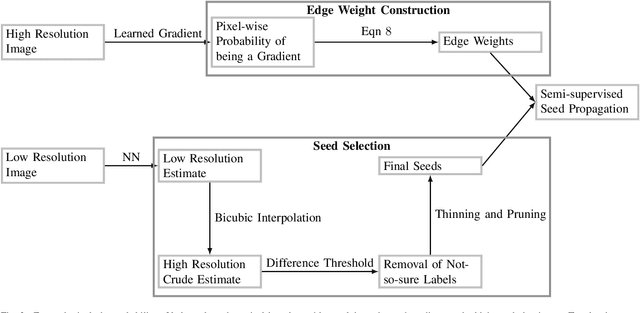
State-of-the-art methods for semantic segmentation of images involve computationally intensive neural network architectures. Most of these methods are not adaptable to high-resolution image segmentation due to memory and other computational issues. Typical approaches in literature involve design of neural network architectures that can fuse global information from low-resolution images and local information from the high-resolution counterparts. However, architectures designed for processing high resolution images are unnecessarily complex and involve a lot of hyper parameters that can be difficult to tune. Also, most of these architectures require ground truth annotations of the high resolution images to train, which can be hard to obtain. In this article, we develop a robust pipeline based on mathematical morphological (MM) operators that can seamlessly extend any existing semantic segmentation algorithm to high resolution images. Our method does not require the ground truth annotations of the high resolution images. It is based on efficiently utilizing information from the low-resolution counterparts, and gradient information on the high-resolution images. We obtain high quality seeds from the inferred labels on low-resolution images using traditional morphological operators and propagate seed labels using a random walker to refine the semantic labels at the boundaries. We show that the semantic segmentation results obtained by our method beat the existing state-of-the-art algorithms on high-resolution images. We empirically prove the robustness of our approach to the hyper parameters used in our pipeline. Further, we characterize some necessary conditions under which our pipeline is applicable and provide an in-depth analysis of the proposed approach.

ESW Edge-Weights : Ensemble Stochastic Watershed Edge-Weights for Hyperspectral Image Classification

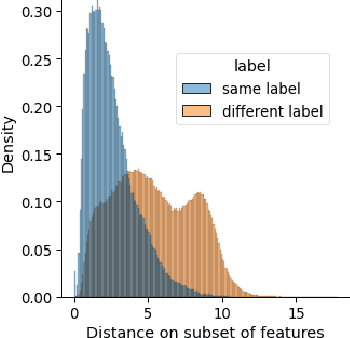
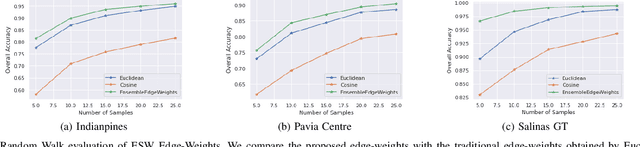
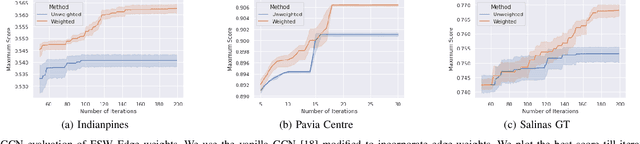
Hyperspectral image (HSI) classification is a topic of active research. One of the main challenges of HSI classification is the lack of reliable labelled samples. Various semi-supervised and unsupervised classification methods are proposed to handle the low number of labelled samples. Chief among them are graph convolution networks (GCN) and their variants. These approaches exploit the graph structure for semi-supervised and unsupervised classification. While several of these methods implicitly construct edge-weights, to our knowledge, not much work has been done to estimate the edge-weights explicitly. In this article, we estimate the edge-weights explicitly and use them for the downstream classification tasks - both semi-supervised and unsupervised. The proposed edge-weights are based on two key insights - (a) Ensembles reduce the variance and (b) Classes in HSI datasets and feature similarity have only one-sided implications. That is, while same classes would have similar features, similar features do not necessarily imply the same classes. Exploiting these, we estimate the edge-weights using an aggregate of ensembles of watersheds over subsamples of features. These edge weights are evaluated for both semi-supervised and unsupervised classification tasks. The evaluation for semi-supervised tasks uses Random-Walk based approach. For the unsupervised case, we use a simple filter using a graph convolution network (GCN). In both these cases, the proposed edge weights outperform the traditional approaches to compute edge-weights - Euclidean distances and cosine similarities. Fascinatingly, with the proposed edge-weights, the simplest GCN obtained results comparable to the recent state-of-the-art.

Higher-Order Relations Skew Link Prediction in Graphs

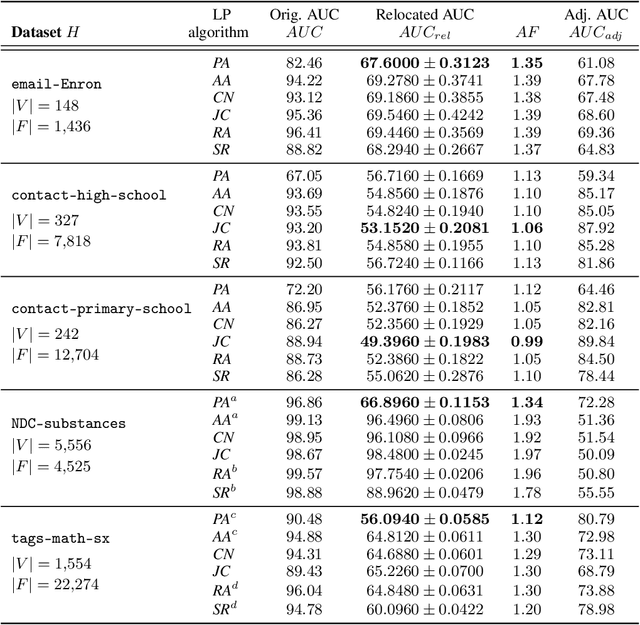
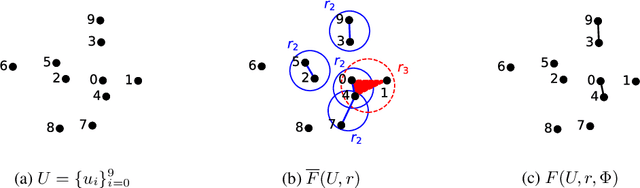
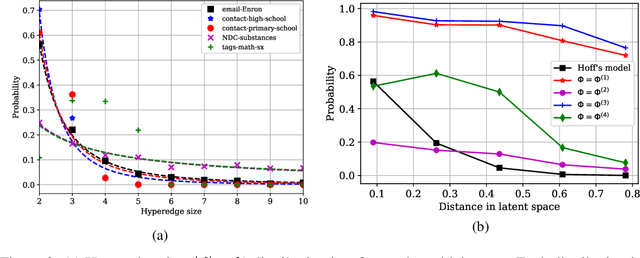
The problem of link prediction is of active interest. The main approach to solving the link prediction problem is based on heuristics such as Common Neighbors (CN) -- more number of common neighbors of a pair of nodes implies a higher chance of them getting linked. In this article, we investigate this problem in the presence of higher-order relations. Surprisingly, it is found that CN works very well, and even better in the presence of higher-order relations. However, as we prove in the current work, this is due to the CN-heuristic overestimating its prediction abilities in the presence of higher-order relations. This statement is proved by considering a theoretical model for higher-order relations and by showing that AUC scores of CN are higher than can be achieved from the model. Theoretical justification in simple cases is also provided. Further, we extend our observations to other similar link prediction algorithms such as Adamic Adar. Finally, these insights are used to propose an adjustment factor by taking into conscience that a random graph would only have a best AUC score of 0.5. This adjustment factor allows for a better estimation of generalization scores.

A Theoretical Analysis of Granulometry-based Roughness Measures on Cartosat DEMs

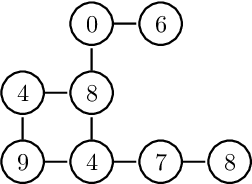
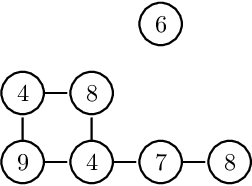
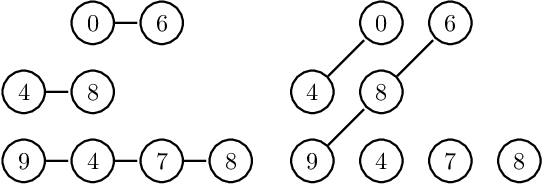
The study of water bodies such as rivers is an important problem in the remote sensing community. A meaningful set of quantitative features reflecting the geophysical properties help us better understand the formation and evolution of rivers. Typically, river sub-basins are analysed using Cartosat Digital Elevation Models (DEMs), obtained at regular time epochs. One of the useful geophysical features of a river sub-basin is that of a roughness measure on DEMs. However, to the best of our knowledge, there is not much literature available on theoretical analysis of roughness measures. In this article, we revisit the roughness measure on DEM data adapted from multiscale granulometries in mathematical morphology, namely multiscale directional granulometric index (MDGI). This measure was classically used to obtain shape-size analysis in greyscale images. In earlier works, MDGIs were introduced to capture the characteristic surficial roughness of a river sub-basin along specific directions. Also, MDGIs can be efficiently computed and are known to be useful features for classification of river sub-basins. In this article, we provide a theoretical analysis of a MDGI. In particular, we characterize non-trivial sufficient conditions on the structure of DEMs under which MDGIs are invariant. These properties are illustrated with some fictitious DEMs. We also provide connections to a discrete derivative of volume of a DEM. Based on these connections, we provide intuition as to why a MDGI is considered a roughness measure. Further, we experimentally illustrate on Lower-Indus, Wardha, and Barmer river sub-basins that the proposed features capture the characteristics of the river sub-basin.

Triplet-Watershed for Hyperspectral Image Classification

Hyperspectral images (HSI) consist of rich spatial and spectral information, which can potentially be used for several applications. However, noise, band correlations and high dimensionality restrict the applicability of such data. This is recently addressed using creative deep learning network architectures such as ResNet, SSRN, and A2S2K. However, the last layer, i.e the classification layer, remains unchanged and is taken to be the softmax classifier. In this article, we propose to use a watershed classifier. Watershed classifier extends the watershed operator from Mathematical Morphology for classification. In its vanilla form, the watershed classifier does not have any trainable parameters. In this article, we propose a novel approach to train deep learning networks to obtain representations suitable for the watershed classifier. The watershed classifier exploits the connectivity patterns, a characteristic of HSI datasets, for better inference. We show that exploiting such characteristics allows the Triplet-Watershed to achieve state-of-art results. These results are validated on Indianpines (IP), University of Pavia (UP), and Kennedy Space Center (KSC) datasets, relying on simple convnet architecture using a quarter of parameters compared to previous state-of-the-art networks.