Higher-Order Relations Skew Link Prediction in Graphs

The problem of link prediction is of active interest. The main approach to solving the link prediction problem is based on heuristics such as Common Neighbors (CN) -- more number of common neighbors of a pair of nodes implies a higher chance of them getting linked. In this article, we investigate this problem in the presence of higher-order relations. Surprisingly, it is found that CN works very well, and even better in the presence of higher-order relations. However, as we prove in the current work, this is due to the CN-heuristic overestimating its prediction abilities in the presence of higher-order relations. This statement is proved by considering a theoretical model for higher-order relations and by showing that AUC scores of CN are higher than can be achieved from the model. Theoretical justification in simple cases is also provided. Further, we extend our observations to other similar link prediction algorithms such as Adamic Adar. Finally, these insights are used to propose an adjustment factor by taking into conscience that a random graph would only have a best AUC score of 0.5. This adjustment factor allows for a better estimation of generalization scores.

Love tHy Neighbour: Remeasuring Local Structural Node Similarity in Hypergraph-Derived Networks

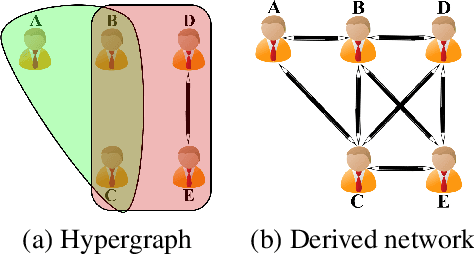
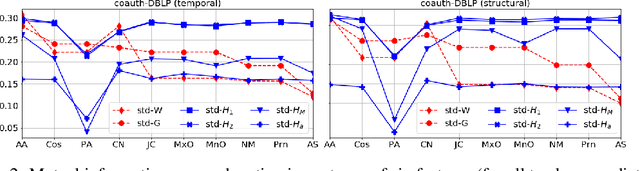
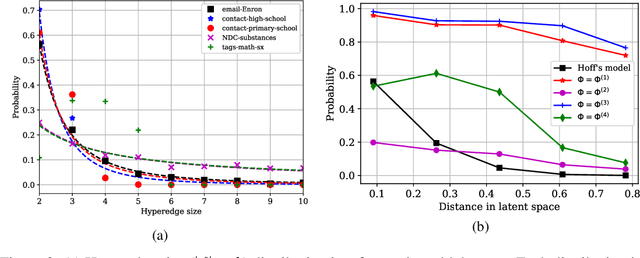
The problem of node-similarity in networks has motivated a plethora of such measures between node-pairs, which make use of the underlying graph structure. However, higher-order relations cannot be losslessly captured by mere graphs and hence, extensions thereof viz. hypergraphs are used instead. Measuring proximity between node pairs in such a setting calls for a revision in the topological measures of similarity, lest the hypergraph structure remains under-exploited. We, in this work, propose a multitude of hypergraph-oriented similarity scores between node-pairs, thereby providing novel solutions to the link prediction problem. As a part of our proposition, we provide theoretical formulations to extend graph-topology based scores to hypergraphs. We compare our scores with graph-based scores (over clique-expansions of hypergraphs into graphs) from the state-of-the-art. Using a combination of the existing graph-based and the proposed hypergraph-based similarity scores as features for a classifier predicts links much better than using the former solely. Experiments on several real-world datasets and both quantitative as well as qualitative analyses on the same exhibit the superiority of the proposed similarity scores over the existing ones.

The CAT SET on the MAT: Cross Attention for Set Matching in Bipartite Hypergraphs

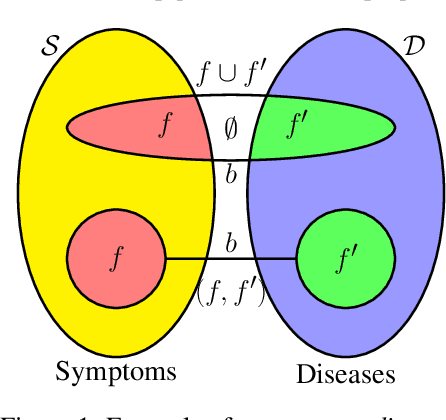
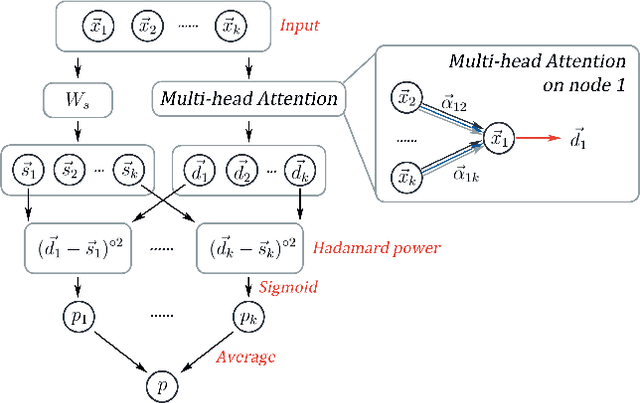
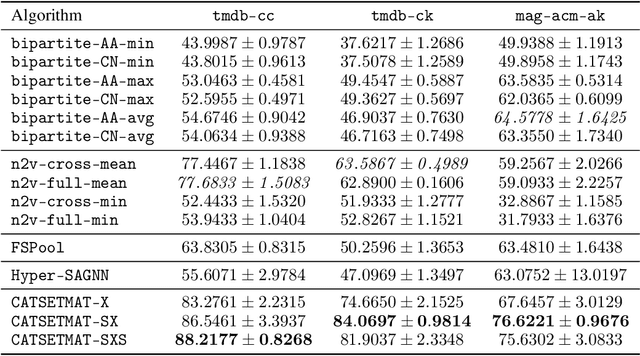
Usual relations between entities could be captured using graphs; but those of a higher-order -- more so between two different types of entities (which we term "left" and "right") -- calls for a "bipartite hypergraph". For example, given a left set of symptoms and right set of diseases, the relation between a set subset of symptoms (that a patient experiences at a given point of time) and a subset of diseases (that he/she might be diagnosed with) could be well-represented using a bipartite hyperedge. The state-of-the-art in embedding nodes of a hypergraph is based on learning the self-attention structure between node-pairs from a hyperedge. In the present work, given a bipartite hypergraph, we aim at capturing relations between node pairs from the cross-product between the left and right hyperedges, and term it a "cross-attention" (CAT) based model. More precisely, we pose "bipartite hyperedge link prediction" as a set-matching (SETMAT) problem and propose a novel neural network architecture called CATSETMAT for the same. We perform extensive experiments on multiple bipartite hypergraph datasets to show the superior performance of CATSETMAT, which we compare with multiple techniques from the state-of-the-art. Our results also elucidate information flow in self- and cross-attention scenarios.