Higher-Order Relations Skew Link Prediction in Graphs
Paper and Code
Oct 30, 2021
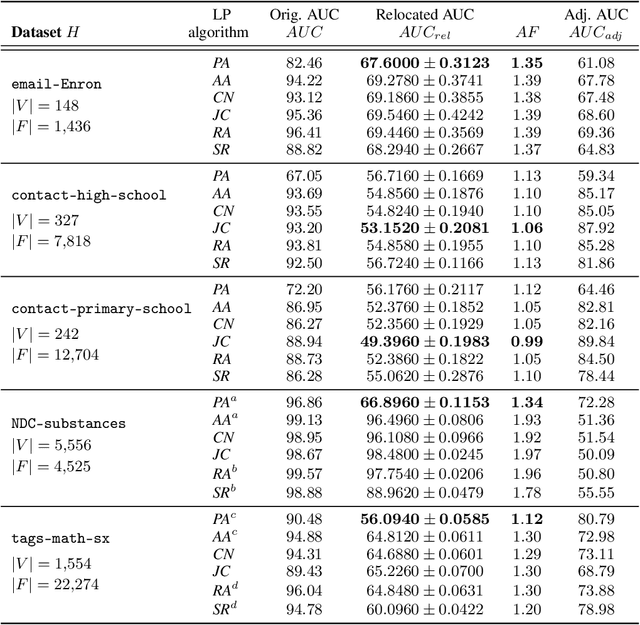
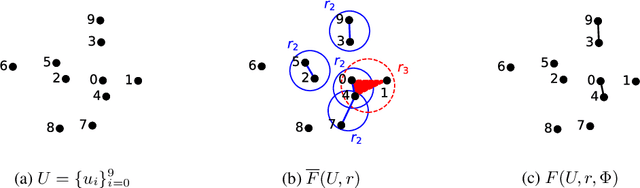
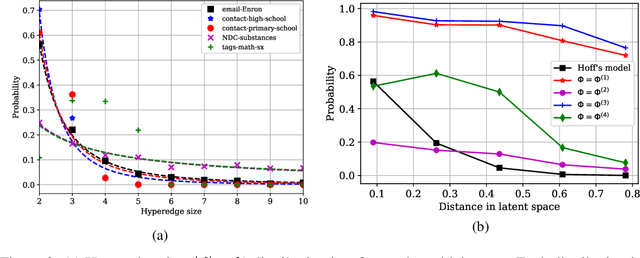
The problem of link prediction is of active interest. The main approach to solving the link prediction problem is based on heuristics such as Common Neighbors (CN) -- more number of common neighbors of a pair of nodes implies a higher chance of them getting linked. In this article, we investigate this problem in the presence of higher-order relations. Surprisingly, it is found that CN works very well, and even better in the presence of higher-order relations. However, as we prove in the current work, this is due to the CN-heuristic overestimating its prediction abilities in the presence of higher-order relations. This statement is proved by considering a theoretical model for higher-order relations and by showing that AUC scores of CN are higher than can be achieved from the model. Theoretical justification in simple cases is also provided. Further, we extend our observations to other similar link prediction algorithms such as Adamic Adar. Finally, these insights are used to propose an adjustment factor by taking into conscience that a random graph would only have a best AUC score of 0.5. This adjustment factor allows for a better estimation of generalization scores.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge