Higher-Order Relations Skew Link Prediction in Graphs

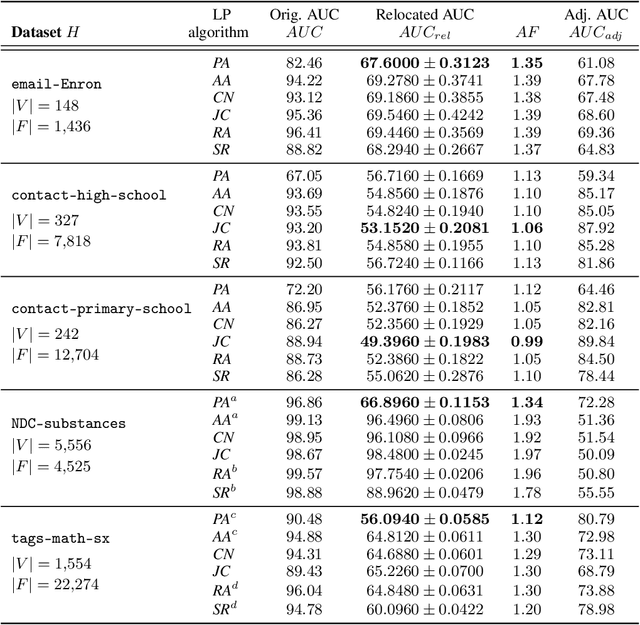
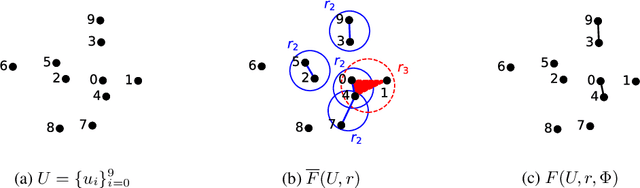
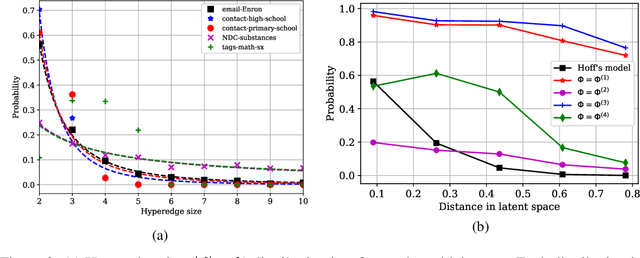
The problem of link prediction is of active interest. The main approach to solving the link prediction problem is based on heuristics such as Common Neighbors (CN) -- more number of common neighbors of a pair of nodes implies a higher chance of them getting linked. In this article, we investigate this problem in the presence of higher-order relations. Surprisingly, it is found that CN works very well, and even better in the presence of higher-order relations. However, as we prove in the current work, this is due to the CN-heuristic overestimating its prediction abilities in the presence of higher-order relations. This statement is proved by considering a theoretical model for higher-order relations and by showing that AUC scores of CN are higher than can be achieved from the model. Theoretical justification in simple cases is also provided. Further, we extend our observations to other similar link prediction algorithms such as Adamic Adar. Finally, these insights are used to propose an adjustment factor by taking into conscience that a random graph would only have a best AUC score of 0.5. This adjustment factor allows for a better estimation of generalization scores.

The CAT SET on the MAT: Cross Attention for Set Matching in Bipartite Hypergraphs

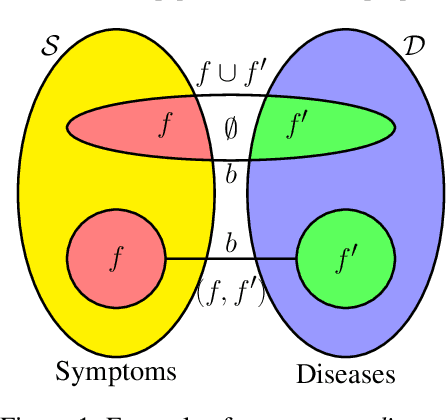
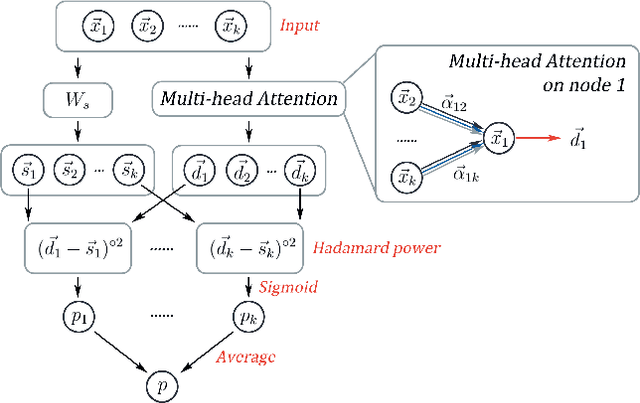
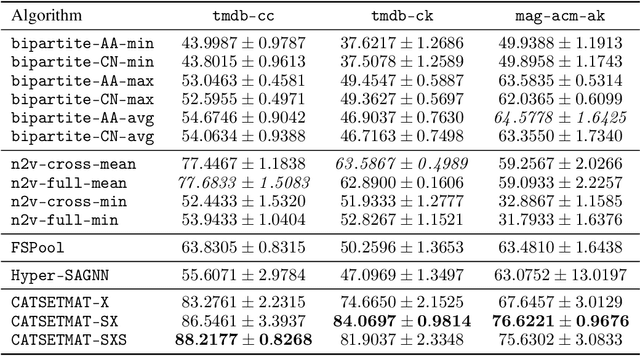
Usual relations between entities could be captured using graphs; but those of a higher-order -- more so between two different types of entities (which we term "left" and "right") -- calls for a "bipartite hypergraph". For example, given a left set of symptoms and right set of diseases, the relation between a set subset of symptoms (that a patient experiences at a given point of time) and a subset of diseases (that he/she might be diagnosed with) could be well-represented using a bipartite hyperedge. The state-of-the-art in embedding nodes of a hypergraph is based on learning the self-attention structure between node-pairs from a hyperedge. In the present work, given a bipartite hypergraph, we aim at capturing relations between node pairs from the cross-product between the left and right hyperedges, and term it a "cross-attention" (CAT) based model. More precisely, we pose "bipartite hyperedge link prediction" as a set-matching (SETMAT) problem and propose a novel neural network architecture called CATSETMAT for the same. We perform extensive experiments on multiple bipartite hypergraph datasets to show the superior performance of CATSETMAT, which we compare with multiple techniques from the state-of-the-art. Our results also elucidate information flow in self- and cross-attention scenarios.

Decentralised Approach for Multi Agent Path Finding

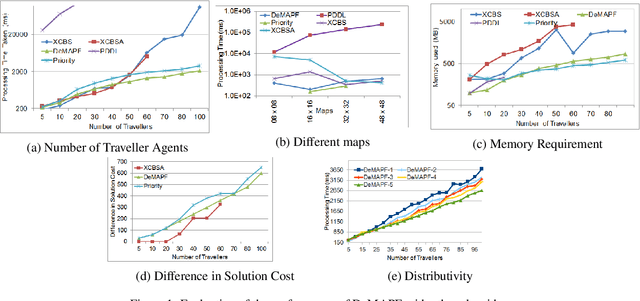
Multi Agent Path Finding (MAPF) requires identification of conflict free paths for agents which could be point-sized or with dimensions. In this paper, we propose an approach for MAPF for spatially-extended agents. These find application in real world problems like Convoy Movement Problem, Train Scheduling etc. Our proposed approach, Decentralised Multi Agent Path Finding (DeMAPF), handles MAPF as a sequence of pathplanning and allocation problems which are solved by two sets of agents Travellers and Routers respectively, over multiple iterations. The approach being decentralised allows an agent to solve the problem pertinent to itself, without being aware of other agents in the same set. This allows the agents to be executed on independent machines, thereby leading to scalability to handle large sized problems. We prove, by comparison with other distributed approaches, that the approach leads to a faster convergence to a conflict-free solution, which may be suboptimal, with lesser memory requirement.

Robust Hierarchical Graph Classification with Subgraph Attention

Graph neural networks get significant attention for graph representation and classification in machine learning community. Attention mechanism applied on the neighborhood of a node improves the performance of graph neural networks. Typically, it helps to identify a neighbor node which plays more important role to determine the label of the node under consideration. But in real world scenarios, a particular subset of nodes together, but not the individual pairs in the subset, may be important to determine the label of the graph. To address this problem, we introduce the concept of subgraph attention for graphs. On the other hand, hierarchical graph pooling has been shown to be promising in recent literature. But due to noisy hierarchical structure of real world graphs, not all the hierarchies of a graph play equal role for graph classification. Towards this end, we propose a graph classification algorithm called SubGattPool which jointly learns the subgraph attention and employs two different types of hierarchical attention mechanisms to find the important nodes in a hierarchy and the importance of individual hierarchies in a graph. Experimental evaluation with different types of graph classification algorithms shows that SubGattPool is able to improve the state-of-the-art or remains competitive on multiple publicly available graph classification datasets. We conduct further experiments on both synthetic and real world graph datasets to justify the usefulness of different components of SubGattPool and to show its consistent performance on other downstream tasks.

Unsupervised Graph Representation by Periphery and Hierarchical Information Maximization

Deep representation learning on non-Euclidean data types, such as graphs, has gained significant attention in recent years. Invent of graph neural networks has improved the state-of-the-art for both node and the entire graph representation in a vector space. However, for the entire graph representation, most of the existing graph neural networks are trained on a graph classification loss in a supervised way. But obtaining labels of a large number of graphs is expensive for real world applications. Thus, we aim to propose an unsupervised graph neural network to generate a vector representation of an entire graph in this paper. For this purpose, we combine the idea of hierarchical graph neural networks and mutual information maximization into a single framework. We also propose and use the concept of periphery representation of a graph and show its usefulness in the proposed algorithm which is referred as GraPHmax. We conduct thorough experiments on several real-world graph datasets and compare the performance of GraPHmax with a diverse set of both supervised and unsupervised baseline algorithms. Experimental results show that we are able to improve the state-of-the-art for multiple graph level tasks on several real-world datasets, while remain competitive on the others.

Line Hypergraph Convolution Network: Applying Graph Convolution for Hypergraphs

Network representation learning and node classification in graphs got significant attention due to the invent of different types graph neural networks. Graph convolution network (GCN) is a popular semi-supervised technique which aggregates attributes within the neighborhood of each node. Conventional GCNs can be applied to simple graphs where each edge connects only two nodes. But many modern days applications need to model high order relationships in a graph. Hypergraphs are effective data types to handle such complex relationships. In this paper, we propose a novel technique to apply graph convolution on hypergraphs with variable hyperedge sizes. We use the classical concept of line graph of a hypergraph for the first time in the hypergraph learning literature. Then we propose to use graph convolution on the line graph of a hypergraph. Experimental analysis on multiple real world network datasets shows the merit of our approach compared to state-of-the-arts.

Cauchy Annealing Schedule: An Annealing Schedule for Boltzmann Selection Scheme in Evolutionary Algorithms

Boltzmann selection is an important selection mechanism in evolutionary algorithms as it has theoretical properties which help in theoretical analysis. However, Boltzmann selection is not used in practice because a good annealing schedule for the `inverse temperature' parameter is lacking. In this paper we propose a Cauchy annealing schedule for Boltzmann selection scheme based on a hypothesis that selection-strength should increase as evolutionary process goes on and distance between two selection strengths should decrease for the process to converge. To formalize these aspects, we develop formalism for selection mechanisms using fitness distributions and give an appropriate measure for selection-strength. In this paper, we prove an important result, by which we derive an annealing schedule called Cauchy annealing schedule. We demonstrate the novelty of proposed annealing schedule using simulations in the framework of genetic algorithms.

Generalized Evolutionary Algorithm based on Tsallis Statistics

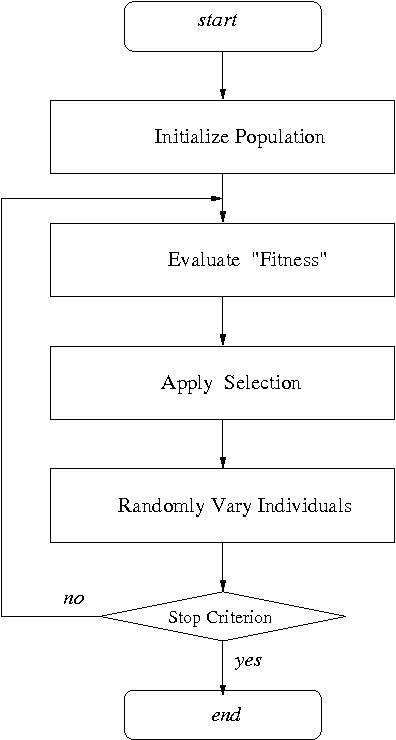
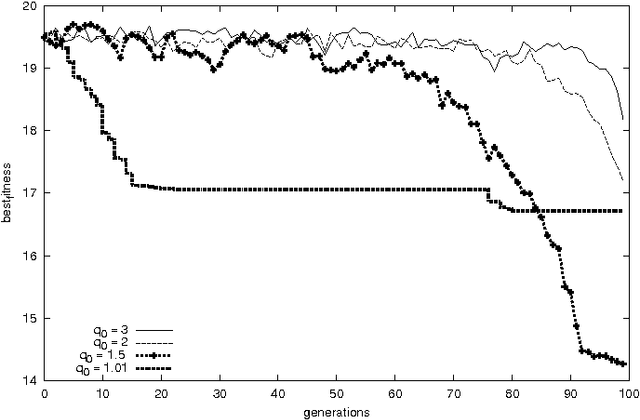
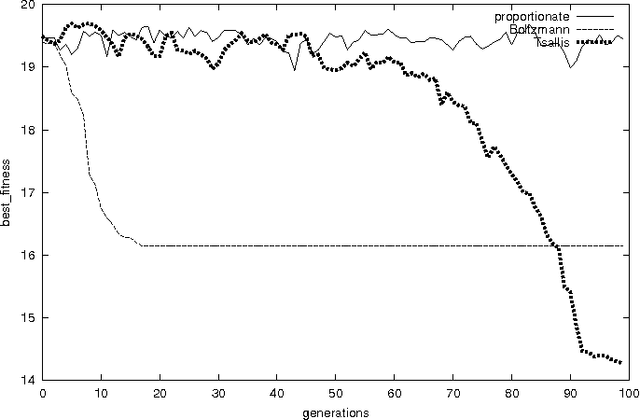
Generalized evolutionary algorithm based on Tsallis canonical distribution is proposed. The algorithm uses Tsallis generalized canonical distribution to weigh the configurations for `selection' instead of Gibbs-Boltzmann distribution. Our simulation results show that for an appropriate choice of non-extensive index that is offered by Tsallis statistics, evolutionary algorithms based on this generalization outperform algorithms based on Gibbs-Boltzmann distribution.