Decoupling Quantile Representations from Loss Functions

The simultaneous quantile regression (SQR) technique has been used to estimate uncertainties for deep learning models, but its application is limited by the requirement that the solution at the median quantile ({\tau} = 0.5) must minimize the mean absolute error (MAE). In this article, we address this limitation by demonstrating a duality between quantiles and estimated probabilities in the case of simultaneous binary quantile regression (SBQR). This allows us to decouple the construction of quantile representations from the loss function, enabling us to assign an arbitrary classifier f(x) at the median quantile and generate the full spectrum of SBQR quantile representations at different {\tau} values. We validate our approach through two applications: (i) detecting out-of-distribution samples, where we show that quantile representations outperform standard probability outputs, and (ii) calibrating models, where we demonstrate the robustness of quantile representations to distortions. We conclude with a discussion of several hypotheses arising from these findings.

Correcting Model Misspecification via Generative Adversarial Networks

Machine learning models are often misspecified in the likelihood, which leads to a lack of robustness in the predictions. In this paper, we introduce a framework for correcting likelihood misspecifications in several paradigm agnostic noisy prior models and test the model's ability to remove the misspecification. The "ABC-GAN" framework introduced is a novel generative modeling paradigm, which combines Generative Adversarial Networks (GANs) and Approximate Bayesian Computation (ABC). This new paradigm assists the existing GANs by incorporating any subjective knowledge available about the modeling process via ABC, as a regularizer, resulting in a partially interpretable model that operates well under low data regimes. At the same time, unlike any Bayesian analysis, the explicit knowledge need not be perfect, since the generator in the GAN can be made arbitrarily complex. ABC-GAN eliminates the need for summary statistics and distance metrics as the discriminator implicitly learns them and enables simultaneous specification of multiple generative models. The model misspecification is simulated in our experiments by introducing noise of various biases and variances. The correction term is learnt via the ABC-GAN, with skip connections, referred to as skipGAN. The strength of the skip connection indicates the amount of correction needed or how misspecified the prior model is. Based on a simple experimental setup, we show that the ABC-GAN models not only correct the misspecification of the prior, but also perform as well as or better than the respective priors under noisier conditions. In this proposal, we show that ABC-GANs get the best of both worlds.

Quantile LSTM: A Robust LSTM for Anomaly Detection In Time Series Data

Anomalies refer to the departure of systems and devices from their normal behaviour in standard operating conditions. An anomaly in an industrial device can indicate an upcoming failure, often in the temporal direction. In this paper, we make two contributions: 1) we estimate conditional quantiles and consider three different ways to define anomalies based on the estimated quantiles. 2) we use a new learnable activation function in the popular Long Short Term Memory networks (LSTM) architecture to model temporal long-range dependency. In particular, we propose Parametric Elliot Function (PEF) as an activation function (AF) inside LSTM, which saturates lately compared to sigmoid and tanh. The proposed algorithms are compared with other well-known anomaly detection algorithms, such as Isolation Forest (iForest), Elliptic Envelope, Autoencoder, and modern Deep Learning models such as Deep Autoencoding Gaussian Mixture Model (DAGMM), Generative Adversarial Networks (GAN). The algorithms are evaluated in terms of various performance metrics, such as Precision and Recall. The algorithms have been tested on multiple industrial time-series datasets such as Yahoo, AWS, GE, and machine sensors. We have found that the LSTM-based quantile algorithms are very effective and outperformed the existing algorithms in identifying anomalies.

Estimation and Applications of Quantiles in Deep Binary Classification

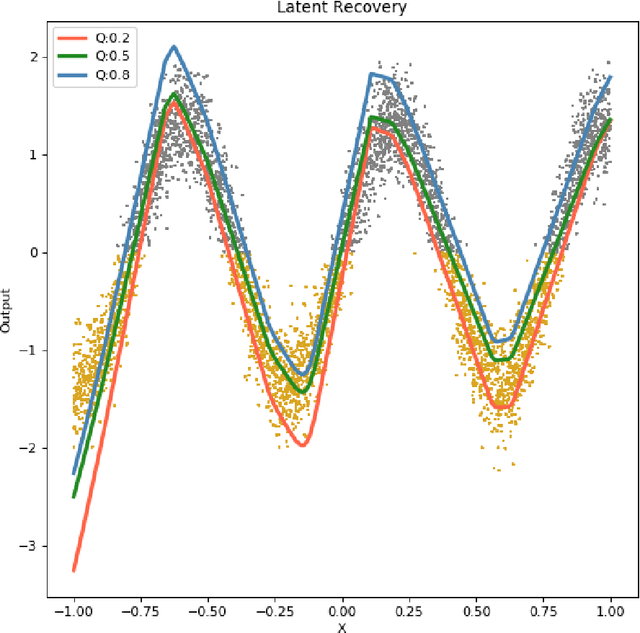
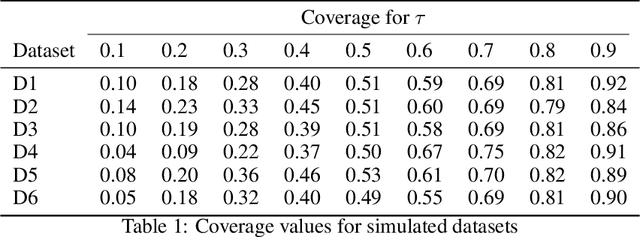
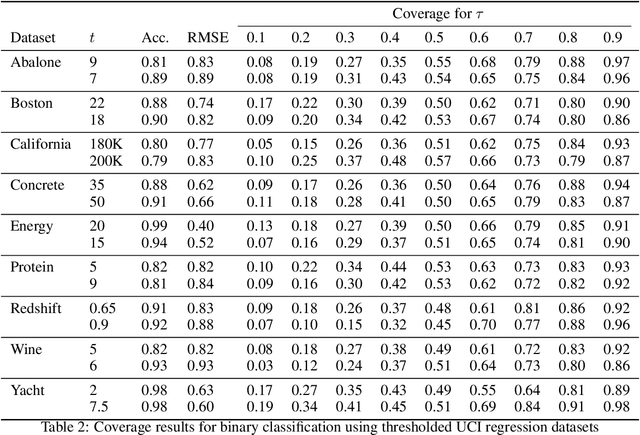
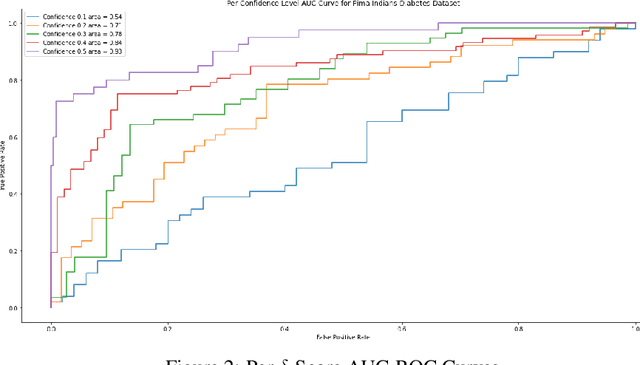
Quantile regression, based on check loss, is a widely used inferential paradigm in Econometrics and Statistics. The conditional quantiles provide a robust alternative to classical conditional means, and also allow uncertainty quantification of the predictions, while making very few distributional assumptions. We consider the analogue of check loss in the binary classification setting. We assume that the conditional quantiles are smooth functions that can be learnt by Deep Neural Networks (DNNs). Subsequently, we compute the Lipschitz constant of the proposed loss, and also show that its curvature is bounded, under some regularity conditions. Consequently, recent results on the error rates and DNN architecture complexity become directly applicable. We quantify the uncertainty of the class probabilities in terms of prediction intervals, and develop individualized confidence scores that can be used to decide whether a prediction is reliable or not at scoring time. By aggregating the confidence scores at the dataset level, we provide two additional metrics, model confidence, and retention rate, to complement the widely used classifier summaries. We also the robustness of the proposed non-parametric binary quantile classification framework are also studied, and we demonstrate how to obtain several univariate summary statistics of the conditional distributions, in particular conditional means, using smoothed conditional quantiles, allowing the use of explanation techniques like Shapley to explain the mean predictions. Finally, we demonstrate an efficient training regime for this loss based on Stochastic Gradient Descent with Lipschitz Adaptive Learning Rates (LALR).