Explaining Puzzle Solutions in Natural Language: An Exploratory Study on 6x6 Sudoku

The success of Large Language Models (LLMs) in human-AI collaborative decision-making hinges on their ability to provide trustworthy, gradual, and tailored explanations. Solving complex puzzles, such as Sudoku, offers a canonical example of this collaboration, where clear and customized explanations often hold greater importance than the final solution. In this study, we evaluate the performance of five LLMs in solving and explaining \sixsix{} Sudoku puzzles. While one LLM demonstrates limited success in solving puzzles, none can explain the solution process in a manner that reflects strategic reasoning or intuitive problem-solving. These findings underscore significant challenges that must be addressed before LLMs can become effective partners in human-AI collaborative decision-making.

Tom: Leveraging trend of the observed gradients for faster convergence

The success of deep learning can be attributed to various factors such as increase in computational power, large datasets, deep convolutional neural networks, optimizers etc. Particularly, the choice of optimizer affects the generalization, convergence rate, and training stability. Stochastic Gradient Descent (SGD) is a first order iterative optimizer that updates the gradient uniformly for all parameters. This uniform update may not be suitable across the entire training phase. A rudimentary solution for this is to employ a fine-tuned learning rate scheduler which decreases learning rate as a function of iteration. To eliminate the dependency of learning rate schedulers, adaptive gradient optimizers such as AdaGrad, AdaDelta, RMSProp, Adam employ a parameter-wise scaling term for learning rate which is a function of the gradient itself. We propose Tom (Trend over Momentum) optimizer, which is a novel variant of Adam that takes into account of the trend which is observed for the gradients in the loss landscape traversed by the neural network. In the proposed Tom optimizer, an additional smoothing equation is introduced to address the trend observed during the process of optimization. The smoothing parameter introduced for the trend requires no tuning and can be used with default values. Experimental results for classification datasets such as CIFAR-10, CIFAR-100 and CINIC-10 image datasets show that Tom outperforms Adagrad, Adadelta, RMSProp and Adam in terms of both accuracy and has a faster convergence. The source code is publicly made available at https://github.com/AnirudhMaiya/Tom

Estimation and Applications of Quantiles in Deep Binary Classification

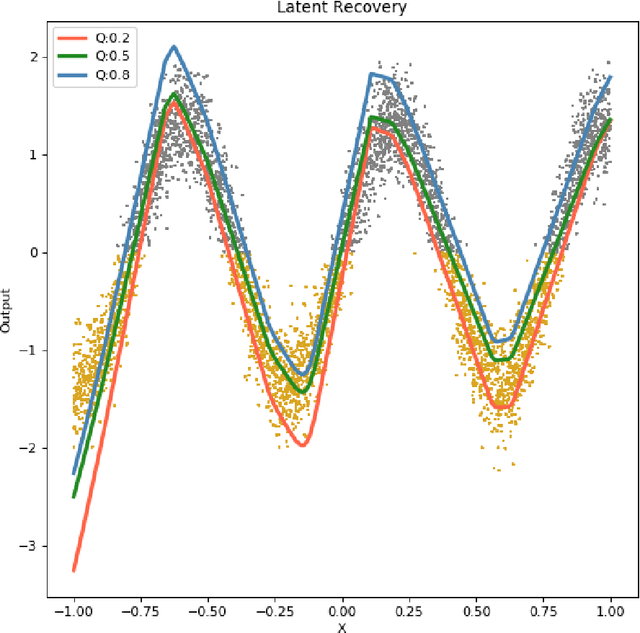
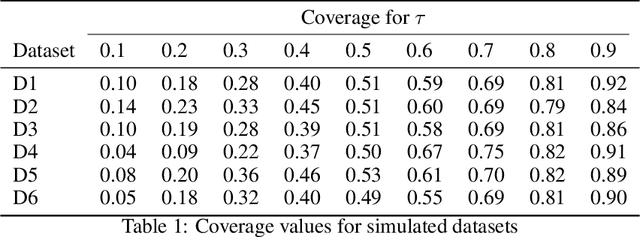
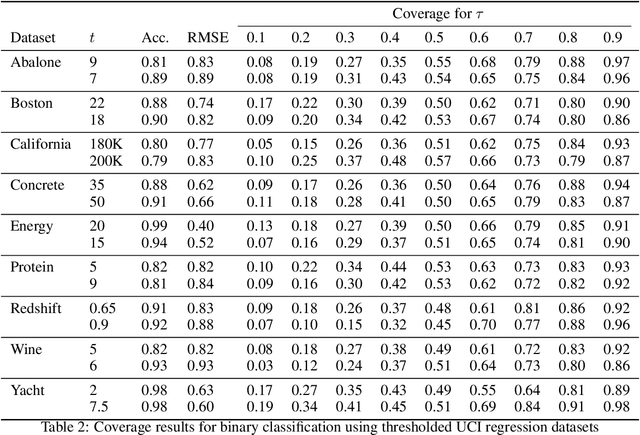
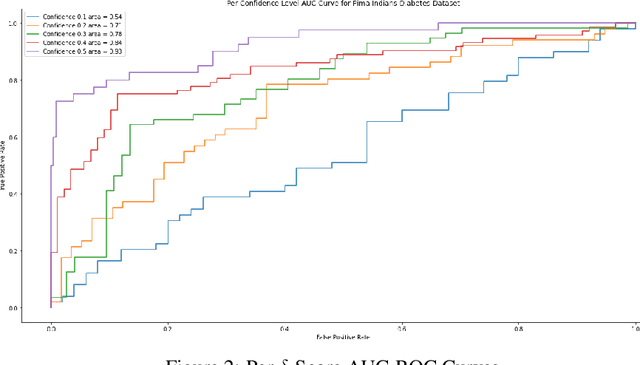
Quantile regression, based on check loss, is a widely used inferential paradigm in Econometrics and Statistics. The conditional quantiles provide a robust alternative to classical conditional means, and also allow uncertainty quantification of the predictions, while making very few distributional assumptions. We consider the analogue of check loss in the binary classification setting. We assume that the conditional quantiles are smooth functions that can be learnt by Deep Neural Networks (DNNs). Subsequently, we compute the Lipschitz constant of the proposed loss, and also show that its curvature is bounded, under some regularity conditions. Consequently, recent results on the error rates and DNN architecture complexity become directly applicable. We quantify the uncertainty of the class probabilities in terms of prediction intervals, and develop individualized confidence scores that can be used to decide whether a prediction is reliable or not at scoring time. By aggregating the confidence scores at the dataset level, we provide two additional metrics, model confidence, and retention rate, to complement the widely used classifier summaries. We also the robustness of the proposed non-parametric binary quantile classification framework are also studied, and we demonstrate how to obtain several univariate summary statistics of the conditional distributions, in particular conditional means, using smoothed conditional quantiles, allowing the use of explanation techniques like Shapley to explain the mean predictions. Finally, we demonstrate an efficient training regime for this loss based on Stochastic Gradient Descent with Lipschitz Adaptive Learning Rates (LALR).