Estimation and Applications of Quantiles in Deep Binary Classification
Paper and Code
Feb 09, 2021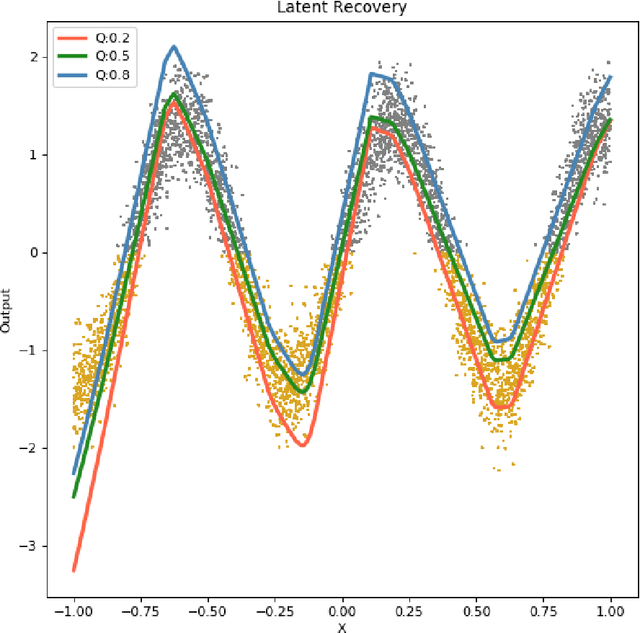
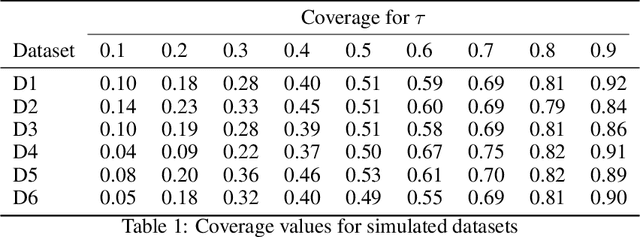
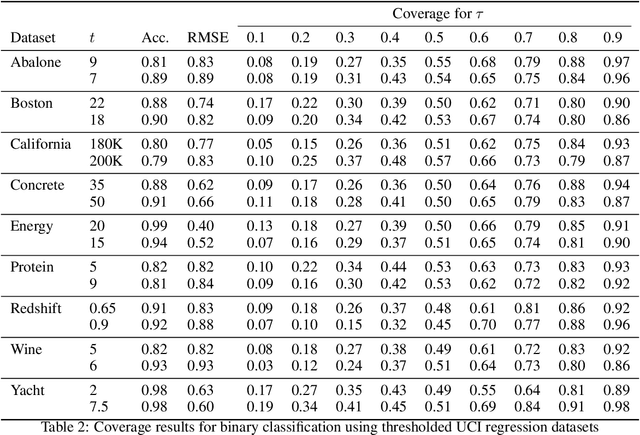
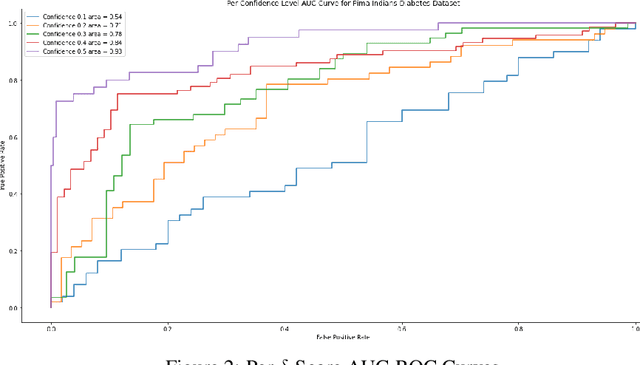
Quantile regression, based on check loss, is a widely used inferential paradigm in Econometrics and Statistics. The conditional quantiles provide a robust alternative to classical conditional means, and also allow uncertainty quantification of the predictions, while making very few distributional assumptions. We consider the analogue of check loss in the binary classification setting. We assume that the conditional quantiles are smooth functions that can be learnt by Deep Neural Networks (DNNs). Subsequently, we compute the Lipschitz constant of the proposed loss, and also show that its curvature is bounded, under some regularity conditions. Consequently, recent results on the error rates and DNN architecture complexity become directly applicable. We quantify the uncertainty of the class probabilities in terms of prediction intervals, and develop individualized confidence scores that can be used to decide whether a prediction is reliable or not at scoring time. By aggregating the confidence scores at the dataset level, we provide two additional metrics, model confidence, and retention rate, to complement the widely used classifier summaries. We also the robustness of the proposed non-parametric binary quantile classification framework are also studied, and we demonstrate how to obtain several univariate summary statistics of the conditional distributions, in particular conditional means, using smoothed conditional quantiles, allowing the use of explanation techniques like Shapley to explain the mean predictions. Finally, we demonstrate an efficient training regime for this loss based on Stochastic Gradient Descent with Lipschitz Adaptive Learning Rates (LALR).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge