ACCO: Accumulate while you Communicate, Hiding Communications in Distributed LLM Training

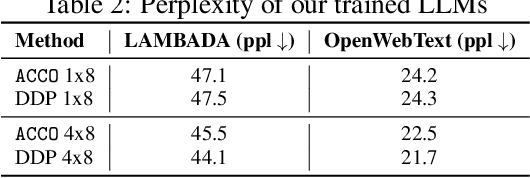
Training Large Language Models (LLMs) relies heavily on distributed implementations, employing multiple GPUs to compute stochastic gradients on model replicas in parallel. However, synchronizing gradients in data parallel settings induces a communication overhead increasing with the number of distributed workers, which can impede the efficiency gains of parallelization. To address this challenge, optimization algorithms reducing inter-worker communication have emerged, such as local optimization methods used in Federated Learning. While effective in minimizing communication overhead, these methods incur significant memory costs, hindering scalability: in addition to extra momentum variables, if communications are only allowed between multiple local optimization steps, then the optimizer's states cannot be sharded among workers. In response, we propose $\textbf{AC}$cumulate while $\textbf{CO}$mmunicate ($\texttt{ACCO}$), a memory-efficient optimization algorithm tailored for distributed training of LLMs. $\texttt{ACCO}$ allows to shard optimizer states across workers, overlaps gradient computations and communications to conceal communication costs, and accommodates heterogeneous hardware. Our method relies on a novel technique to mitigate the one-step delay inherent in parallel execution of gradient computations and communications, eliminating the need for warmup steps and aligning with the training dynamics of standard distributed optimization while converging faster in terms of wall-clock time. We demonstrate the effectiveness of $\texttt{ACCO}$ on several LLMs training and fine-tuning tasks.

WASH: Train your Ensemble with Communication-Efficient Weight Shuffling, then Average

The performance of deep neural networks is enhanced by ensemble methods, which average the output of several models. However, this comes at an increased cost at inference. Weight averaging methods aim at balancing the generalization of ensembling and the inference speed of a single model by averaging the parameters of an ensemble of models. Yet, naive averaging results in poor performance as models converge to different loss basins, and aligning the models to improve the performance of the average is challenging. Alternatively, inspired by distributed training, methods like DART and PAPA have been proposed to train several models in parallel such that they will end up in the same basin, resulting in good averaging accuracy. However, these methods either compromise ensembling accuracy or demand significant communication between models during training. In this paper, we introduce WASH, a novel distributed method for training model ensembles for weight averaging that achieves state-of-the-art image classification accuracy. WASH maintains models within the same basin by randomly shuffling a small percentage of weights during training, resulting in diverse models and lower communication costs compared to standard parameter averaging methods.

$\textbf{A}^2\textbf{CiD}^2$: Accelerating Asynchronous Communication in Decentralized Deep Learning

Distributed training of Deep Learning models has been critical to many recent successes in the field. Current standard methods primarily rely on synchronous centralized algorithms which induce major communication bottlenecks and limit their usability to High-Performance Computing (HPC) environments with strong connectivity. Decentralized asynchronous algorithms are emerging as a potential alternative but their practical applicability still lags. In this work, we focus on peerto-peer asynchronous methods due to their flexibility and parallelization potentials. In order to mitigate the increase in bandwidth they require at large scale and in poorly connected contexts, we introduce a principled asynchronous, randomized, gossip-based algorithm which works thanks to a continuous momentum named $\textbf{A}^2\textbf{CiD}^2$. In addition to inducing a significant communication acceleration at no cost other than doubling the parameters, minimal adaptation is required to incorporate $\textbf{A}^2\textbf{CiD}^2$ to other asynchronous approaches. We demonstrate its efficiency theoretically and numerically. Empirically on the ring graph, adding $\textbf{A}^2\textbf{CiD}^2$ has the same effect as doubling the communication rate. In particular, we show consistent improvement on the ImageNet dataset using up to 64 asynchronous workers (A100 GPUs) and various communication network topologies.

DADAO: Decoupled Accelerated Decentralized Asynchronous Optimization for Time-Varying Gossips

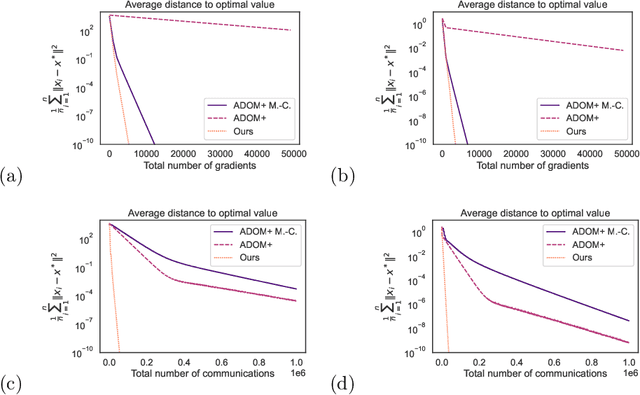
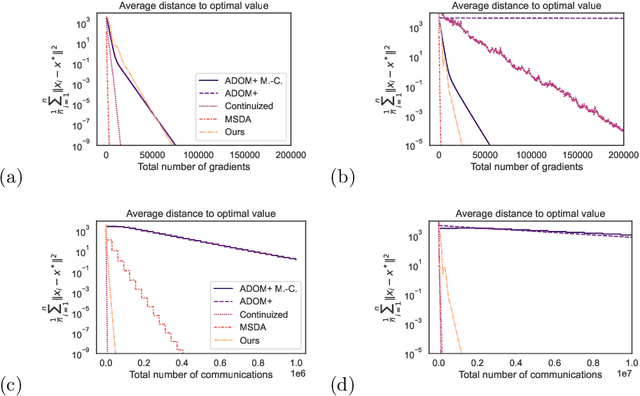
DADAO is a novel decentralized asynchronous stochastic algorithm to minimize a sum of $L$-smooth and $\mu$-strongly convex functions distributed over a time-varying connectivity network of size $n$. We model the local gradient updates and gossip communication procedures with separate independent Poisson Point Processes, decoupling the computation and communication steps in addition to making the whole approach completely asynchronous. Our method employs primal gradients and do not use a multi-consensus inner loop nor other ad-hoc mechanisms as Error Feedback, Gradient Tracking or a Proximal operator. By relating spatial quantities of our graphs $\chi^*_1,\chi_2^*$ to a necessary minimal communication rate between nodes of the network, we show that our algorithm requires $\mathcal{O}(n\sqrt{\frac{L}{\mu}}\log \epsilon)$ local gradients and only $\mathcal{O}(n\sqrt{\chi_1^*\chi_2^*}\sqrt{\frac{L}{\mu}}\log \epsilon)$ communications to reach a precision $\epsilon$. If SGD with uniform noise $\sigma^2$ is used, we reach a precision $\epsilon$ with same speed, up to a bias term in $\mathcal{O}(\frac{\sigma^2}{\sqrt{\mu L}})$. This improves upon the bounds obtained with current state-of-the-art approaches, our simulations validating the strength of our relatively unconstrained method. Our source-code is released on a public repository.

Speech Sequence Embeddings using Nearest Neighbors Contrastive Learning

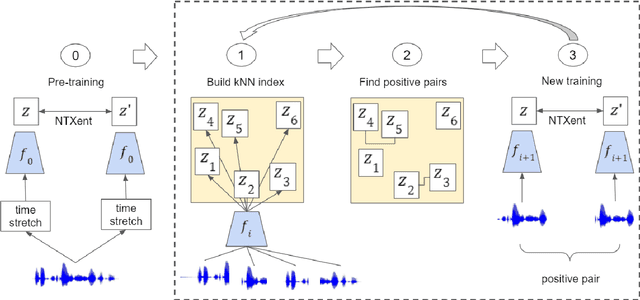
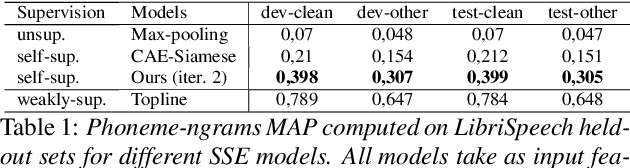
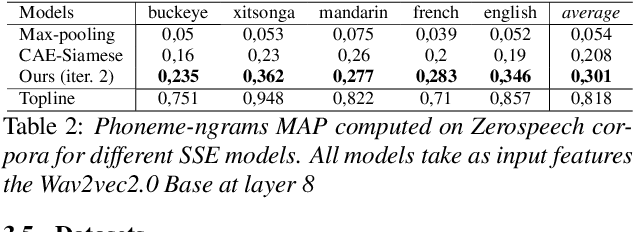
We introduce a simple neural encoder architecture that can be trained using an unsupervised contrastive learning objective which gets its positive samples from data-augmented k-Nearest Neighbors search. We show that when built on top of recent self-supervised audio representations, this method can be applied iteratively and yield competitive SSE as evaluated on two tasks: query-by-example of random sequences of speech, and spoken term discovery. On both tasks our method pushes the state-of-the-art by a significant margin across 5 different languages. Finally, we establish a benchmark on a query-by-example task on the LibriSpeech dataset to monitor future improvements in the field.

Curriculum learning for multilevel budgeted combinatorial problems

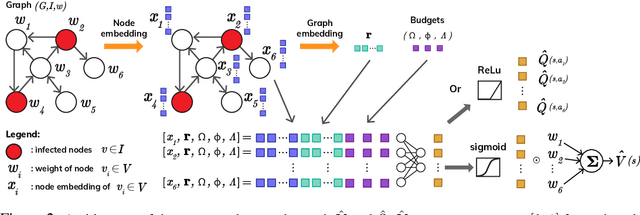
Learning heuristics for combinatorial optimization problems through graph neural networks have recently shown promising results on some classic NP-hard problems. These are single-level optimization problems with only one player. Multilevel combinatorial optimization problems are their generalization, encompassing situations with multiple players taking decisions sequentially. By framing them in a multi-agent reinforcement learning setting, we devise a value-based method to learn to solve multilevel budgeted combinatorial problems involving two players in a zero-sum game over a graph. Our framework is based on a simple curriculum: if an agent knows how to estimate the value of instances with budgets up to $B$, then solving instances with budget $B+1$ can be done in polynomial time regardless of the direction of the optimization by checking the value of every possible afterstate. Thus, in a bottom-up approach, we generate datasets of heuristically solved instances with increasingly larger budgets to train our agent. We report results close to optimality on graphs up to $100$ nodes and a $185 \times$ speedup on average compared to the quickest exact solver known for the Multilevel Critical Node problem, a max-min-max trilevel problem that has been shown to be at least $\Sigma_2^p$-hard.