DADAO: Decoupled Accelerated Decentralized Asynchronous Optimization for Time-Varying Gossips
Paper and Code
Jul 26, 2022
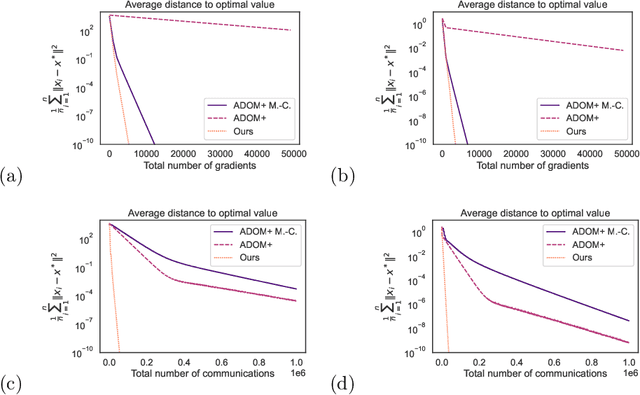

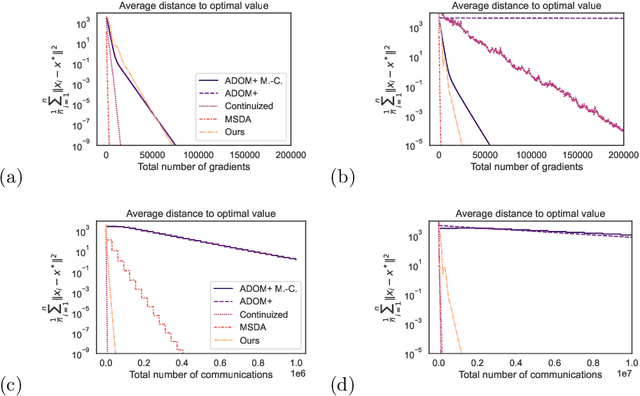
DADAO is a novel decentralized asynchronous stochastic algorithm to minimize a sum of $L$-smooth and $\mu$-strongly convex functions distributed over a time-varying connectivity network of size $n$. We model the local gradient updates and gossip communication procedures with separate independent Poisson Point Processes, decoupling the computation and communication steps in addition to making the whole approach completely asynchronous. Our method employs primal gradients and do not use a multi-consensus inner loop nor other ad-hoc mechanisms as Error Feedback, Gradient Tracking or a Proximal operator. By relating spatial quantities of our graphs $\chi^*_1,\chi_2^*$ to a necessary minimal communication rate between nodes of the network, we show that our algorithm requires $\mathcal{O}(n\sqrt{\frac{L}{\mu}}\log \epsilon)$ local gradients and only $\mathcal{O}(n\sqrt{\chi_1^*\chi_2^*}\sqrt{\frac{L}{\mu}}\log \epsilon)$ communications to reach a precision $\epsilon$. If SGD with uniform noise $\sigma^2$ is used, we reach a precision $\epsilon$ with same speed, up to a bias term in $\mathcal{O}(\frac{\sigma^2}{\sqrt{\mu L}})$. This improves upon the bounds obtained with current state-of-the-art approaches, our simulations validating the strength of our relatively unconstrained method. Our source-code is released on a public repository.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge