Continual Learning with Guarantees via Weight Interval Constraints

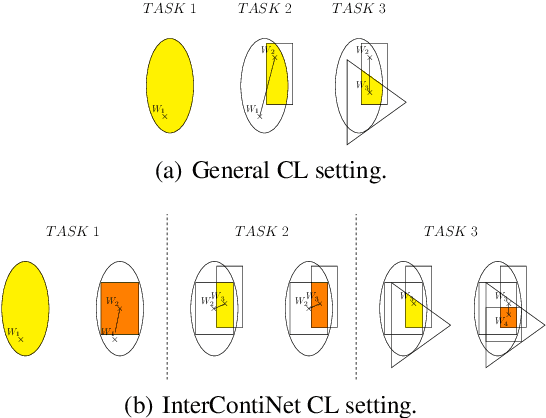
We introduce a new training paradigm that enforces interval constraints on neural network parameter space to control forgetting. Contemporary Continual Learning (CL) methods focus on training neural networks efficiently from a stream of data, while reducing the negative impact of catastrophic forgetting, yet they do not provide any firm guarantees that network performance will not deteriorate uncontrollably over time. In this work, we show how to put bounds on forgetting by reformulating continual learning of a model as a continual contraction of its parameter space. To that end, we propose Hyperrectangle Training, a new training methodology where each task is represented by a hyperrectangle in the parameter space, fully contained in the hyperrectangles of the previous tasks. This formulation reduces the NP-hard CL problem back to polynomial time while providing full resilience against forgetting. We validate our claim by developing InterContiNet (Interval Continual Learning) algorithm which leverages interval arithmetic to effectively model parameter regions as hyperrectangles. Through experimental results, we show that our approach performs well in a continual learning setup without storing data from previous tasks.

Target Layer Regularization for Continual Learning Using Cramer-Wold Generator

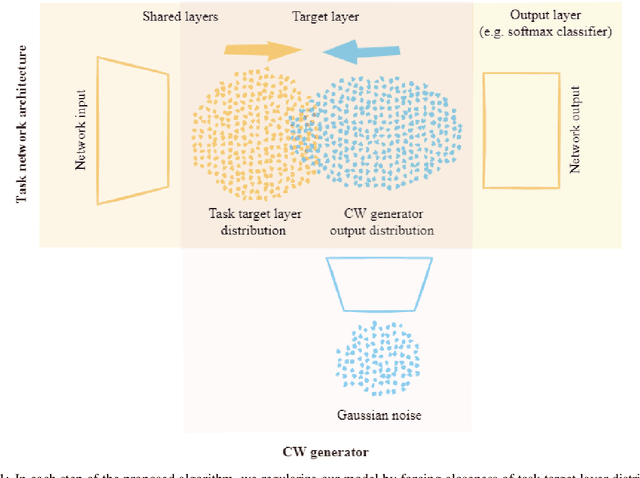
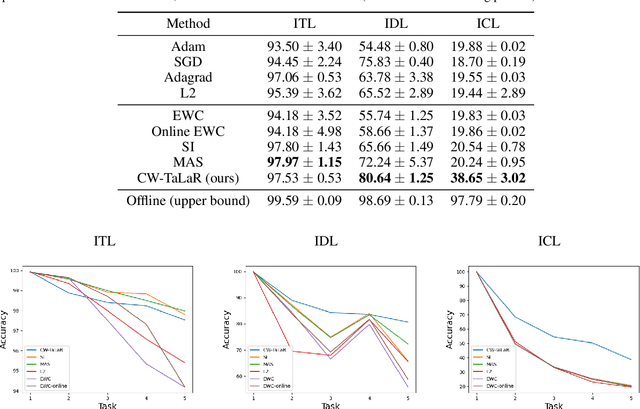
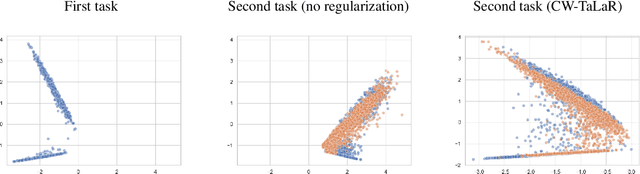
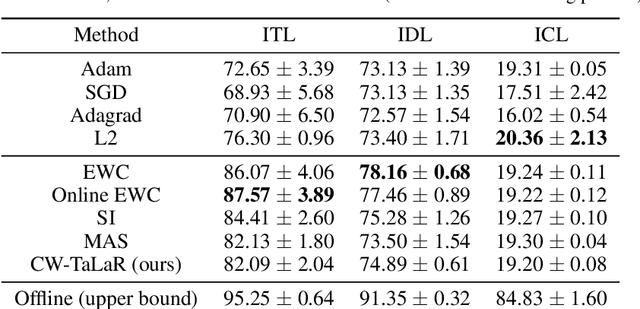
We propose an effective regularization strategy (CW-TaLaR) for solving continual learning problems. It uses a penalizing term expressed by the Cramer-Wold distance between two probability distributions defined on a target layer of an underlying neural network that is shared by all tasks, and the simple architecture of the Cramer-Wold generator for modeling output data representation. Our strategy preserves target layer distribution while learning a new task but does not require remembering previous tasks' datasets. We perform experiments involving several common supervised frameworks, which prove the competitiveness of the CW-TaLaR method in comparison to a few existing state-of-the-art continual learning models.