Train Faster, Perform Better: Modular Adaptive Training in Over-Parameterized Models
Paper and Code
May 13, 2024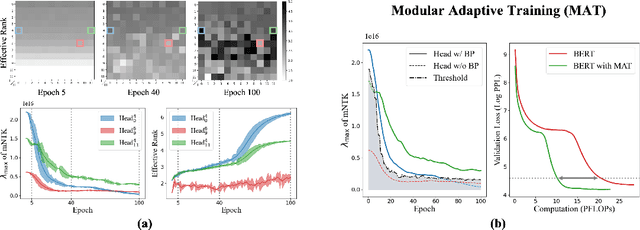

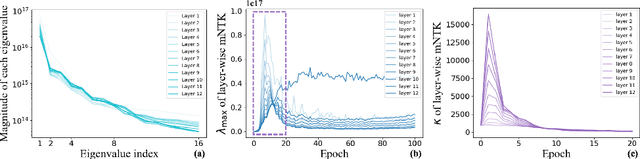

Despite their prevalence in deep-learning communities, over-parameterized models convey high demands of computational costs for proper training. This work studies the fine-grained, modular-level learning dynamics of over-parameterized models to attain a more efficient and fruitful training strategy. Empirical evidence reveals that when scaling down into network modules, such as heads in self-attention models, we can observe varying learning patterns implicitly associated with each module's trainability. To describe such modular-level learning capabilities, we introduce a novel concept dubbed modular neural tangent kernel (mNTK), and we demonstrate that the quality of a module's learning is tightly associated with its mNTK's principal eigenvalue $\lambda_{\max}$. A large $\lambda_{\max}$ indicates that the module learns features with better convergence, while those miniature ones may impact generalization negatively. Inspired by the discovery, we propose a novel training strategy termed Modular Adaptive Training (MAT) to update those modules with their $\lambda_{\max}$ exceeding a dynamic threshold selectively, concentrating the model on learning common features and ignoring those inconsistent ones. Unlike most existing training schemes with a complete BP cycle across all network modules, MAT can significantly save computations by its partially-updating strategy and can further improve performance. Experiments show that MAT nearly halves the computational cost of model training and outperforms the accuracy of baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge