A Policy Gradient Algorithm for Learning to Learn in Multiagent Reinforcement Learning

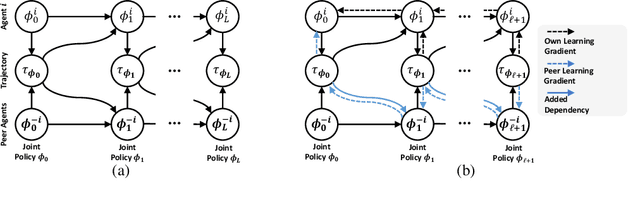
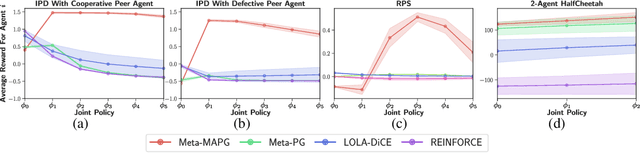
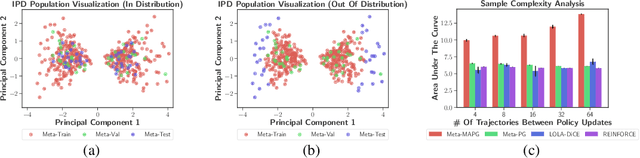
A fundamental challenge in multiagent reinforcement learning is to learn beneficial behaviors in a shared environment with other agents that are also simultaneously learning. In particular, each agent perceives the environment as effectively non-stationary due to the changing policies of other agents. Moreover, each agent is itself constantly learning, leading to natural nonstationarity in the distribution of experiences encountered. In this paper, we propose a novel meta-multiagent policy gradient theorem that directly accommodates for the non-stationary policy dynamics inherent to these multiagent settings. This is achieved by modeling our gradient updates to directly consider both an agent's own non-stationary policy dynamics and the non-stationary policy dynamics of other agents interacting with it in the environment. We find that our theoretically grounded approach provides a general solution to the multiagent learning problem, which inherently combines key aspects of previous state of the art approaches on this topic. We test our method on several multiagent benchmarks and demonstrate a more efficient ability to adapt to new agents as they learn than previous related approaches across the spectrum of mixed incentive, competitive, and cooperative environments.