From Off-Policy to On-Policy: Enhancing GUI Agents via Bi-level Expert-to-Policy Assimilation

Vision-language models are increasingly deployed as computer-use agents (CUAs) that operate desktops and browsers. Top-performing CUAs are framework-based systems that decompose planning and execution, while end-to-end screenshot-to-action policies are easier to deploy but lag behind on benchmarks such as OSWorld-Verified. GUI datasets like OSWorld pose two bottlenecks: they expose only a few hundred interactive, verifiable tasks and environments, and expert trajectories must be gathered by interacting with these environments, making such data hard to scale. We therefore ask how reinforcement learning from verifiable rewards (RLVR) can best exploit a small pool of exist expert trajectories to train end-to-end policies. Naively mixing these off-policy traces into on-policy RLVR is brittle: even after format conversion, expert trajectories exhibit structural mismatch and distribution shift from the learner. We propose BEPA (Bi-Level Expert-to-Policy Assimilation), which turns static expert traces into policy-aligned guidance via self-rolled reachable trajectories under the base policy (LEVEL-1) and a per-task, dynamically updated cache used in RLVR (LEVEL-2). On OSWorld-Verified, BEPA improves UITARS1.5-7B success from 22.87% to 32.13% and raises a held-out split from 5.74% to 10.30%, with consistent gains on MMBench-GUI and Online-Mind2Web. Our code and data are available at: https://github.com/LEON-gittech/Verl_GUI.git

InfiniteWeb: Scalable Web Environment Synthesis for GUI Agent Training

GUI agents that interact with graphical interfaces on behalf of users represent a promising direction for practical AI assistants. However, training such agents is hindered by the scarcity of suitable environments. We present InfiniteWeb, a system that automatically generates functional web environments at scale for GUI agent training. While LLMs perform well on generating a single webpage, building a realistic and functional website with many interconnected pages faces challenges. We address these challenges through unified specification, task-centric test-driven development, and a combination of website seed with reference design image to ensure diversity. Our system also generates verifiable task evaluators enabling dense reward signals for reinforcement learning. Experiments show that InfiniteWeb surpasses commercial coding agents at realistic website construction, and GUI agents trained on our generated environments achieve significant performance improvements on OSWorld and Online-Mind2Web, demonstrating the effectiveness of proposed system.

UI-Evol: Automatic Knowledge Evolving for Computer Use Agents

External knowledge has played a crucial role in the recent development of computer use agents. We identify a critical knowledge-execution gap: retrieved knowledge often fails to translate into effective real-world task execution. Our analysis shows even 90\% correct knowledge yields only 41\% execution success rate. To bridge this gap, we propose UI-Evol, a plug-and-play module for autonomous GUI knowledge evolution. UI-Evol consists of two stages: a Retrace Stage that extracts faithful objective action sequences from actual agent-environment interactions, and a Critique Stage that refines existing knowledge by comparing these sequences against external references. We conduct comprehensive experiments on the OSWorld benchmark with the state-of-the-art Agent S2. Our results demonstrate that UI-Evol not only significantly boosts task performance but also addresses a previously overlooked issue of high behavioral standard deviation in computer use agents, leading to superior performance on computer use tasks and substantially improved agent reliability.

UI-E2I-Synth: Advancing GUI Grounding with Large-Scale Instruction Synthesis

Recent advancements in Large Vision-Language Models are accelerating the development of Graphical User Interface (GUI) agents that utilize human-like vision perception capabilities to enhance productivity on digital devices. Compared to approaches predicated on GUI metadata, which are platform-dependent and vulnerable to implementation variations, vision-based approaches offer broader applicability. In this vision-based paradigm, the GUI instruction grounding, which maps user instruction to the location of corresponding element on the given screenshot, remains a critical challenge, particularly due to limited public training dataset and resource-intensive manual instruction data annotation. In this paper, we delve into unexplored challenges in this task including element-to-screen ratio, unbalanced element type, and implicit instruction. To address these challenges, we introduce a large-scale data synthesis pipeline UI-E2I-Synth for generating varying complex instruction datasets using GPT-4o instead of human annotators. Furthermore, we propose a new GUI instruction grounding benchmark UI-I2E-Bench, which is designed to address the limitations of existing benchmarks by incorporating diverse annotation aspects. Our model, trained on the synthesized data, achieves superior performance in GUI instruction grounding, demonstrating the advancements of proposed data synthesis pipeline. The proposed benchmark, accompanied by extensive analyses, provides practical insights for future research in GUI grounding. We will release corresponding artifacts at https://colmon46.github.io/i2e-bench-leaderboard/ .

Asymptotic Escape of Spurious Critical Points on the Low-rank Matrix Manifold

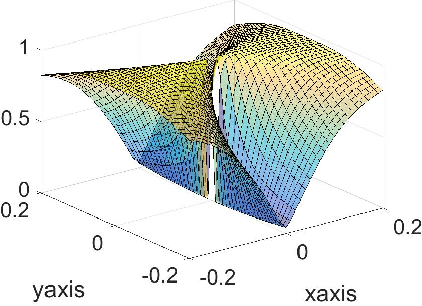
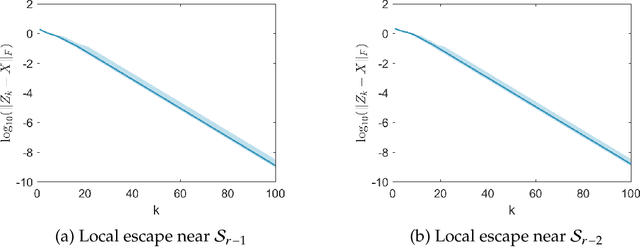
We show that the Riemannian gradient descent algorithm on the low-rank matrix manifold almost surely escapes some spurious critical points on the boundary of the manifold. Given that the low-rank matrix manifold is an incomplete set, this result is the first to overcome this difficulty and partially justify the global use of the Riemannian gradient descent on the manifold. The spurious critical points are some rank-deficient matrices that capture only part of the SVD components of the ground truth. They exhibit very singular behavior and evade the classical analysis of strict saddle points. We show that using the dynamical low-rank approximation and a rescaled gradient flow, some of the spurious critical points can be converted to classical strict saddle points, which leads to the desired result. Numerical experiments are provided to support our theoretical findings.

Fast Global Convergence for Low-rank Matrix Recovery via Riemannian Gradient Descent with Random Initialization

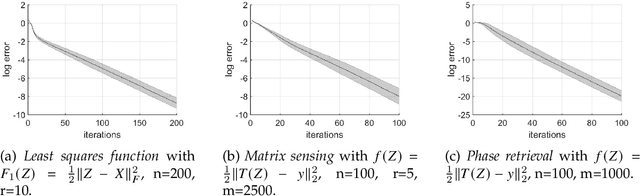
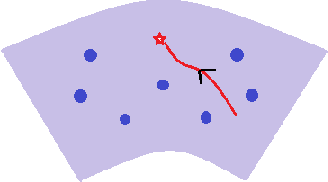
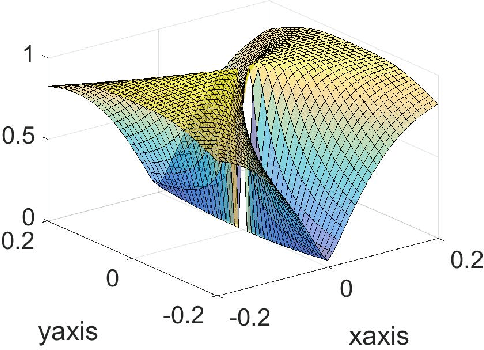
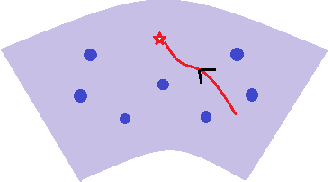
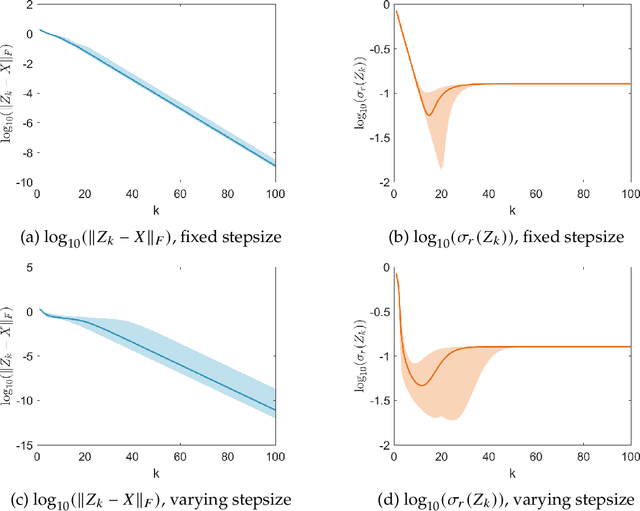
In this paper, we propose a new global analysis framework for a class of low-rank matrix recovery problems on the Riemannian manifold. We analyze the global behavior for the Riemannian optimization with random initialization. We use the Riemannian gradient descent algorithm to minimize a least squares loss function, and study the asymptotic behavior as well as the exact convergence rate. We reveal a previously unknown geometric property of the low-rank matrix manifold, which is the existence of spurious critical points for the simple least squares function on the manifold. We show that under some assumptions, the Riemannian gradient descent starting from a random initialization with high probability avoids these spurious critical points and only converges to the ground truth in nearly linear convergence rate, i.e. $\mathcal{O}(\text{log}(\frac{1}{\epsilon})+ \text{log}(n))$ iterations to reach an $\epsilon$-accurate solution. We use two applications as examples for our global analysis. The first one is a rank-1 matrix recovery problem. The second one is the Gaussian phase retrieval problem. The second example only satisfies the weak isometry property, but has behavior similar to that of the first one except for an extra saddle set. Our convergence guarantee is nearly optimal and almost dimension-free, which fully explains the numerical observations. The global analysis can be potentially extended to other data problems with random measurement structures and empirical least squares loss functions.

A Fast Hierarchically Preconditioned Eigensolver Based On Multiresolution Matrix Decomposition

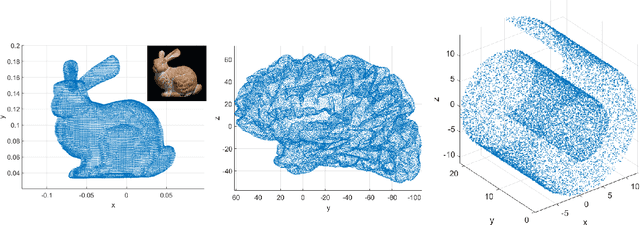
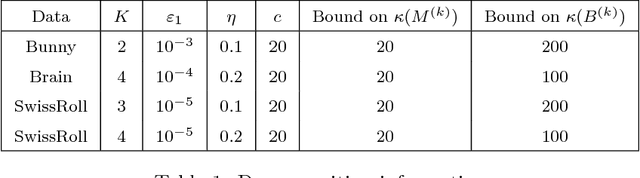
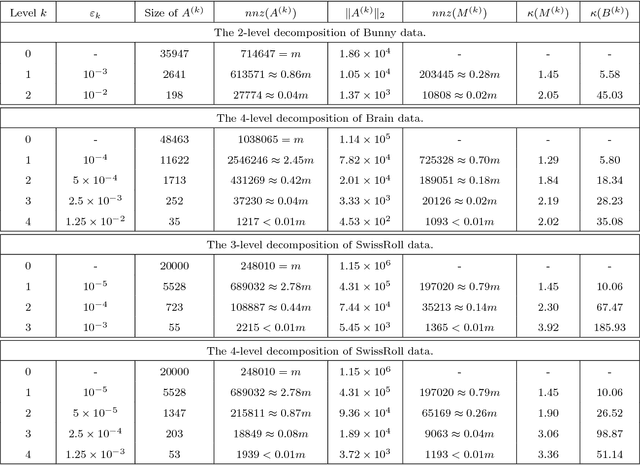
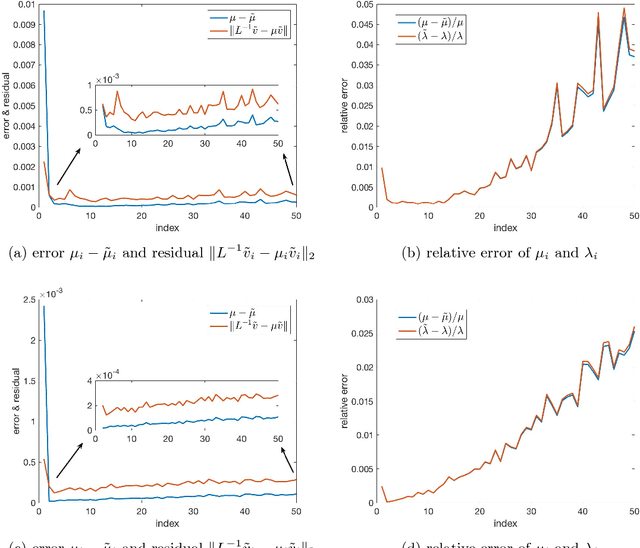
In this paper we propose a new iterative method to hierarchically compute a relatively large number of leftmost eigenpairs of a sparse symmetric positive matrix under the multiresolution operator compression framework. We exploit the well-conditioned property of every decomposition components by integrating the multiresolution framework into the Implicitly restarted Lanczos method. We achieve this combination by proposing an extension-refinement iterative scheme, in which the intrinsic idea is to decompose the target spectrum into several segments such that the corresponding eigenproblem in each segment is well-conditioned. Theoretical analysis and numerical illustration are also reported to illustrate the efficiency and effectiveness of this algorithm.