De Huang
Streaming k-PCA: Efficient guarantees for Oja's algorithm, beyond rank-one updates
Feb 06, 2021Abstract:We analyze Oja's algorithm for streaming $k$-PCA and prove that it achieves performance nearly matching that of an optimal offline algorithm. Given access to a sequence of i.i.d. $d \times d$ symmetric matrices, we show that Oja's algorithm can obtain an accurate approximation to the subspace of the top $k$ eigenvectors of their expectation using a number of samples that scales polylogarithmically with $d$. Previously, such a result was only known in the case where the updates have rank one. Our analysis is based on recently developed matrix concentration tools, which allow us to prove strong bounds on the tails of the random matrices which arise in the course of the algorithm's execution.
A Fast Hierarchically Preconditioned Eigensolver Based On Multiresolution Matrix Decomposition
Jun 27, 2018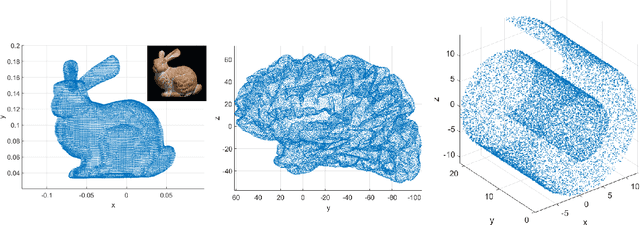
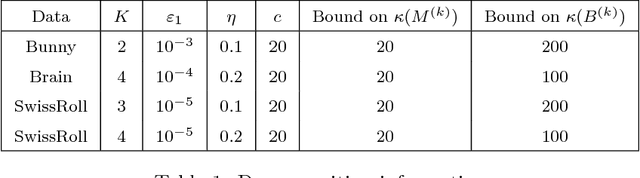
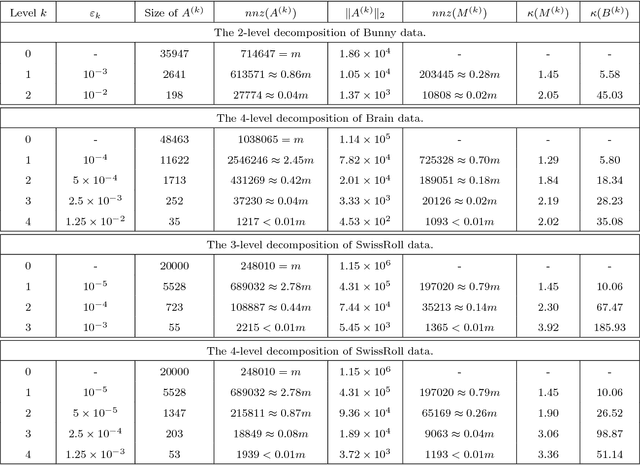
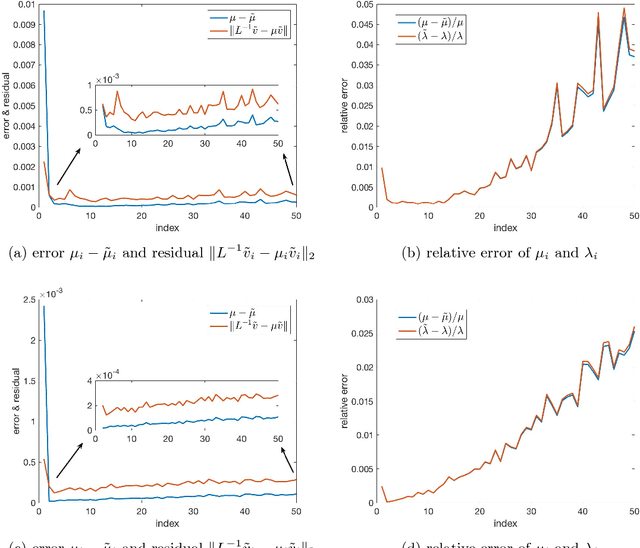
Abstract:In this paper we propose a new iterative method to hierarchically compute a relatively large number of leftmost eigenpairs of a sparse symmetric positive matrix under the multiresolution operator compression framework. We exploit the well-conditioned property of every decomposition components by integrating the multiresolution framework into the Implicitly restarted Lanczos method. We achieve this combination by proposing an extension-refinement iterative scheme, in which the intrinsic idea is to decompose the target spectrum into several segments such that the corresponding eigenproblem in each segment is well-conditioned. Theoretical analysis and numerical illustration are also reported to illustrate the efficiency and effectiveness of this algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge