A Fast Hierarchically Preconditioned Eigensolver Based On Multiresolution Matrix Decomposition
Paper and Code
Jun 27, 2018
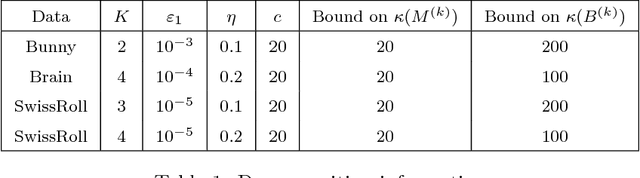
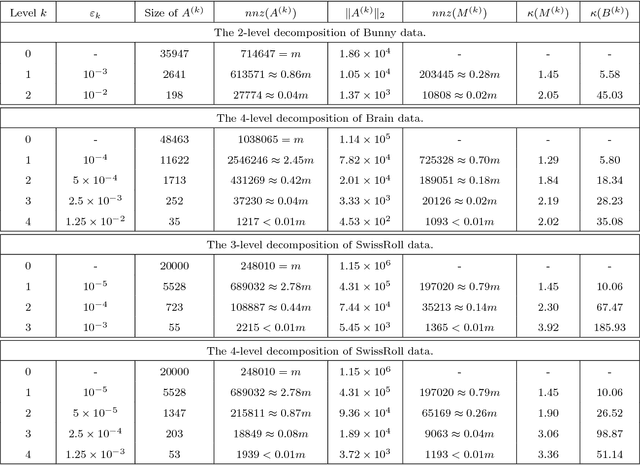
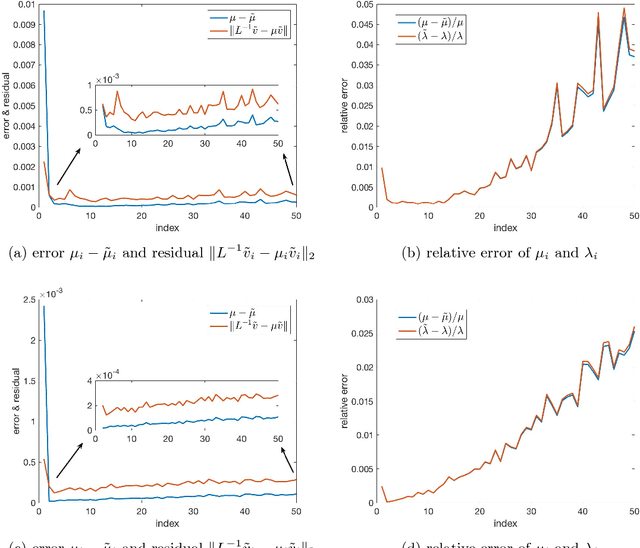
In this paper we propose a new iterative method to hierarchically compute a relatively large number of leftmost eigenpairs of a sparse symmetric positive matrix under the multiresolution operator compression framework. We exploit the well-conditioned property of every decomposition components by integrating the multiresolution framework into the Implicitly restarted Lanczos method. We achieve this combination by proposing an extension-refinement iterative scheme, in which the intrinsic idea is to decompose the target spectrum into several segments such that the corresponding eigenproblem in each segment is well-conditioned. Theoretical analysis and numerical illustration are also reported to illustrate the efficiency and effectiveness of this algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge