Boosting Out-of-Distribution Detection with Multiple Pre-trained Models

Out-of-Distribution (OOD) detection, i.e., identifying whether an input is sampled from a novel distribution other than the training distribution, is a critical task for safely deploying machine learning systems in the open world. Recently, post hoc detection utilizing pre-trained models has shown promising performance and can be scaled to large-scale problems. This advance raises a natural question: Can we leverage the diversity of multiple pre-trained models to improve the performance of post hoc detection methods? In this work, we propose a detection enhancement method by ensembling multiple detection decisions derived from a zoo of pre-trained models. Our approach uses the p-value instead of the commonly used hard threshold and leverages a fundamental framework of multiple hypothesis testing to control the true positive rate of In-Distribution (ID) data. We focus on the usage of model zoos and provide systematic empirical comparisons with current state-of-the-art methods on various OOD detection benchmarks. The proposed ensemble scheme shows consistent improvement compared to single-model detectors and significantly outperforms the current competitive methods. Our method substantially improves the relative performance by 65.40% and 26.96% on the CIFAR10 and ImageNet benchmarks.

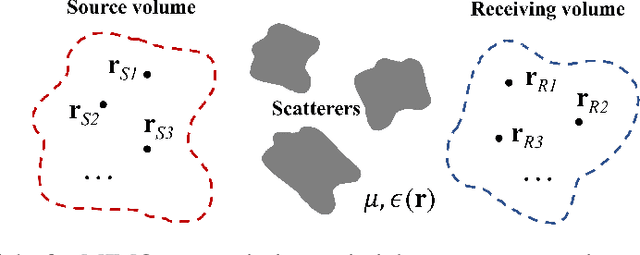
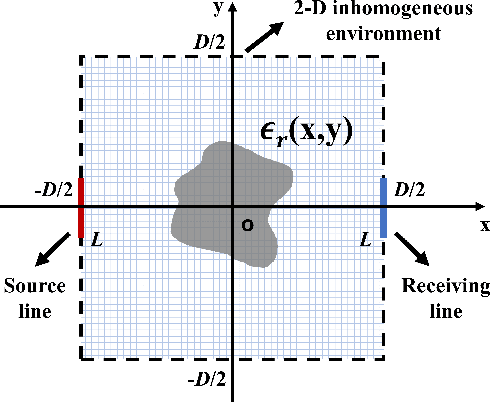
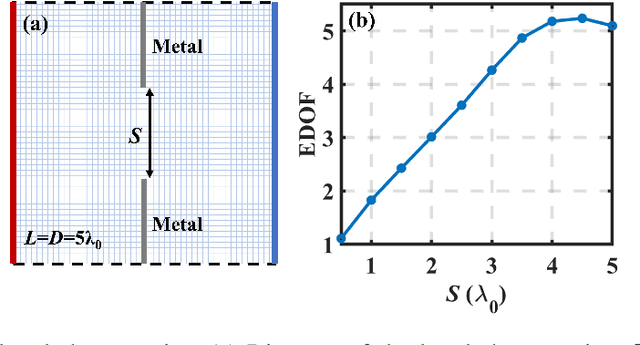
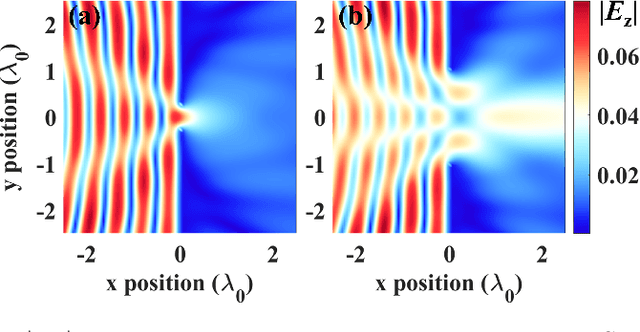
Electromagnetic Effective-Degree-of-Freedom Limit of a MIMO System in 2-D Inhomogeneous Environment

Compared with a single-input-single-output (SISO) wireless communication system, the benefit of multiple-input-multiple-output (MIMO) technology originates from its extra degree of freedom (DOF), also referred as scattering channels or spatial electromagnetic (EM) modes, brought by spatial multiplexing. When the physical sizes of transmitting and receiving arrays are fixed, and there are sufficient antennas (typically with half-wavelength spacings), the DOF limit is only dependent on the propagating environment. Analytical methods can be used to estimate this limit in free space, and some approximate models are adopted in stochastic environments, such as Clarke's model and Ray-tracing methods. However, this DOF limit in an certain inhomogeneous environment has not been well discussed with rigorous full-wave numerical methods. In this work, volume integral equation (VIE) is implemented for investigating the limit of MIMO effective degree of freedom (EDOF) in three representative two-dimensional (2-D) inhomogeneous environments. Moreover, we clarify the relation between the performance of a MIMO system and the scattering characteristics of its propagating environment.

Electromagnetic Effective Degree of Freedom of a MIMO System in Free Space

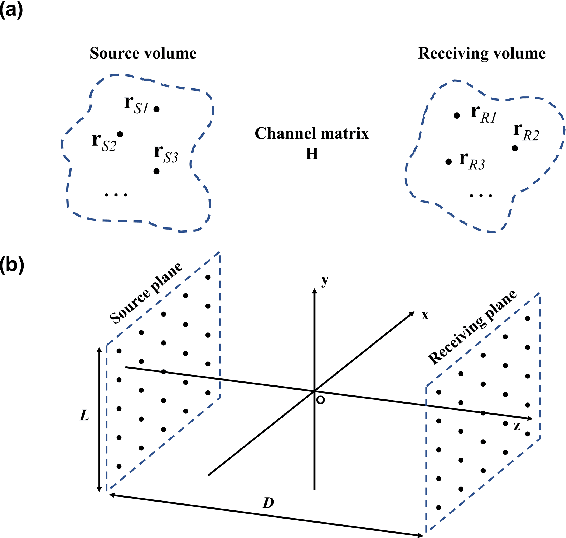
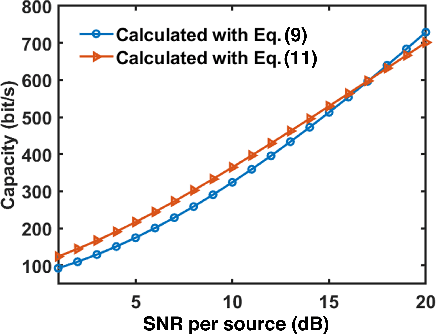
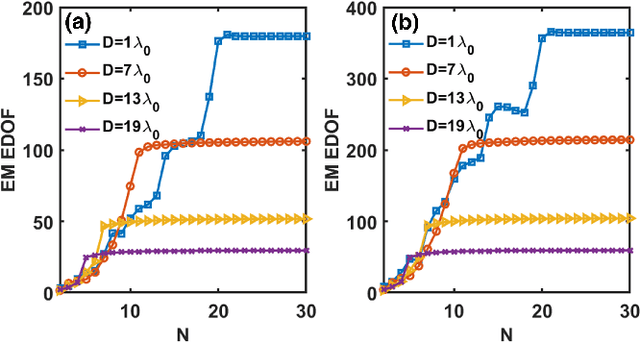
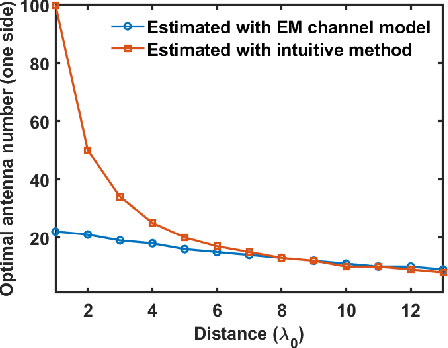
Effective degree of freedom (EDOF) of a multiple-input-multiple-output (MIMO) system represents its equivalent number of independent single-input-single-output (SISO) systems, which directly characterizes the communication performance. Traditional EDOF only considers single polarization, where the full polarized components degrade into two independent transverse components under the far-field approximation. However, the traditional model is not applicable to complex scenarios especially for the near-field region. Based on an electromagnetic (EM) channel model built from the dyadic Green's function, we first calculate the EM EDOF to estimate the performance of an arbitrary MIMO system with full polarizations in free space. Then, we clarify the relations between the limit of EDOF and the optimal number of sources/receivers. Finally, potential benefits of near-field MIMO communications are demonstrated with the EM EDOF, in which the contribution of the longitudinally polarized source is taken into account. This work establishes a fundamental EM framework for MIMO wireless communications.