Towards Better Understanding of In-Context Learning Ability from In-Context Uncertainty Quantification

Predicting simple function classes has been widely used as a testbed for developing theory and understanding of the trained Transformer's in-context learning (ICL) ability. In this paper, we revisit the training of Transformers on linear regression tasks, and different from all the existing literature, we consider a bi-objective prediction task of predicting both the conditional expectation $\mathbb{E}[Y|X]$ and the conditional variance Var$(Y|X)$. This additional uncertainty quantification objective provides a handle to (i) better design out-of-distribution experiments to distinguish ICL from in-weight learning (IWL) and (ii) make a better separation between the algorithms with and without using the prior information of the training distribution. Theoretically, we show that the trained Transformer reaches near Bayes-optimum, suggesting the usage of the information of the training distribution. Our method can be extended to other cases. Specifically, with the Transformer's context window $S$, we prove a generalization bound of $\tilde{\mathcal{O}}(\sqrt{\min\{S, T\}/(n T)})$ on $n$ tasks with sequences of length $T$, providing sharper analysis compared to previous results of $\tilde{\mathcal{O}}(\sqrt{1/n})$. Empirically, we illustrate that while the trained Transformer behaves as the Bayes-optimal solution as a natural consequence of supervised training in distribution, it does not necessarily perform a Bayesian inference when facing task shifts, in contrast to the \textit{equivalence} between these two proposed in many existing literature. We also demonstrate the trained Transformer's ICL ability over covariates shift and prompt-length shift and interpret them as a generalization over a meta distribution.

Towards Better Statistical Understanding of Watermarking LLMs

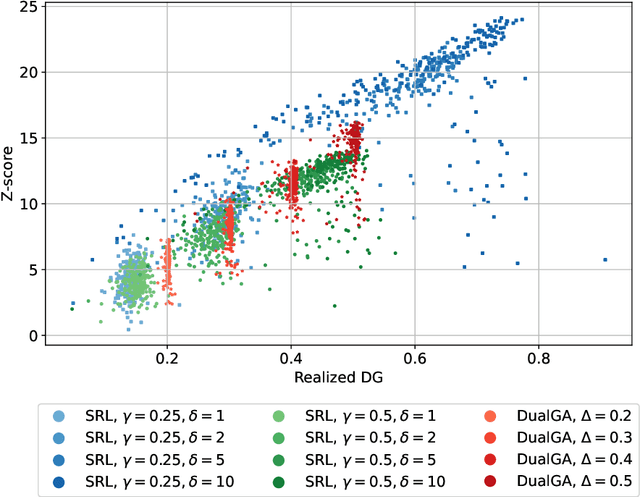
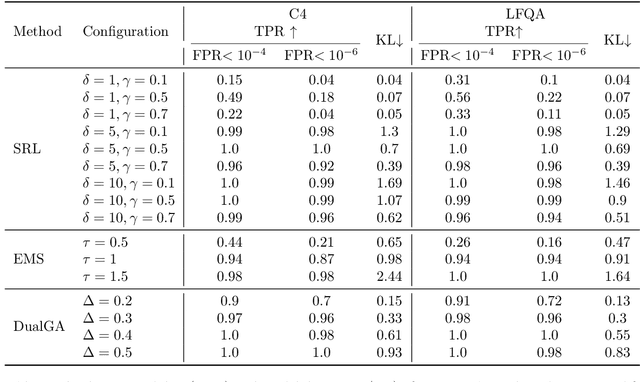
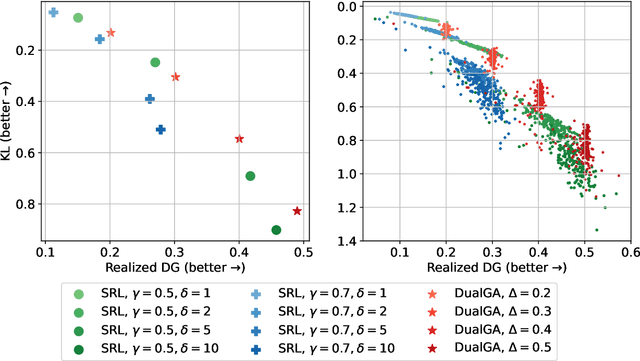
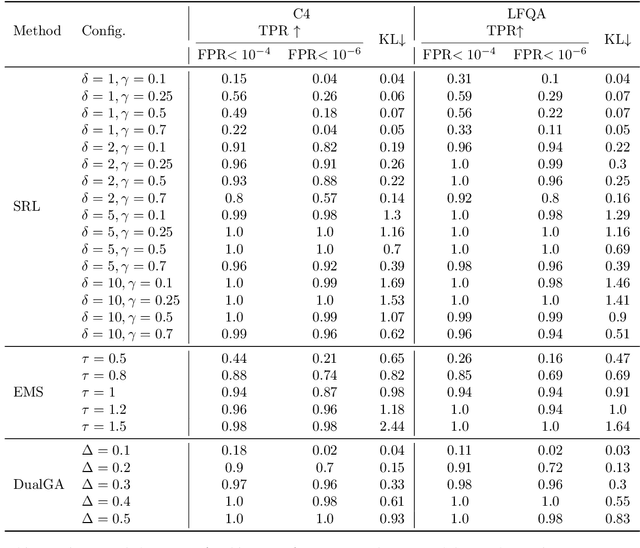
In this paper, we study the problem of watermarking large language models (LLMs). We consider the trade-off between model distortion and detection ability and formulate it as a constrained optimization problem based on the green-red algorithm of Kirchenbauer et al. (2023a). We show that the optimal solution to the optimization problem enjoys a nice analytical property which provides a better understanding and inspires the algorithm design for the watermarking process. We develop an online dual gradient ascent watermarking algorithm in light of this optimization formulation and prove its asymptotic Pareto optimality between model distortion and detection ability. Such a result guarantees an averaged increased green list probability and henceforth detection ability explicitly (in contrast to previous results). Moreover, we provide a systematic discussion on the choice of the model distortion metrics for the watermarking problem. We justify our choice of KL divergence and present issues with the existing criteria of ``distortion-free'' and perplexity. Finally, we empirically evaluate our algorithms on extensive datasets against benchmark algorithms.

A Neural Network Based Choice Model for Assortment Optimization

Discrete-choice models are used in economics, marketing and revenue management to predict customer purchase probabilities, say as a function of prices and other features of the offered assortment. While they have been shown to be expressive, capturing customer heterogeneity and behaviour, they are also hard to estimate, often based on many unobservables like utilities; and moreover, they still fail to capture many salient features of customer behaviour. A natural question then, given their success in other contexts, is if neural networks can eliminate the necessity of carefully building a context-dependent customer behaviour model and hand-coding and tuning the estimation. It is unclear however how one would incorporate assortment effects into such a neural network, and also how one would optimize the assortment with such a black-box generative model of choice probabilities. In this paper we investigate first whether a single neural network architecture can predict purchase probabilities for datasets from various contexts and generated under various models and assumptions. Next, we develop an assortment optimization formulation that is solvable by off-the-shelf integer programming solvers. We compare against a variety of benchmark discrete-choice models on simulated as well as real-world datasets, developing training tricks along the way to make the neural network prediction and subsequent optimization robust and comparable in performance to the alternates.

Distribution-Free Model-Agnostic Regression Calibration via Nonparametric Methods

In this paper, we consider the uncertainty quantification problem for regression models. Specifically, we consider an individual calibration objective for characterizing the quantiles of the prediction model. While such an objective is well-motivated from downstream tasks such as newsvendor cost, the existing methods have been largely heuristic and lack of statistical guarantee in terms of individual calibration. We show via simple examples that the existing methods focusing on population-level calibration guarantees such as average calibration or sharpness can lead to harmful and unexpected results. We propose simple nonparametric calibration methods that are agnostic of the underlying prediction model and enjoy both computational efficiency and statistical consistency. Our approach enables a better understanding of the possibility of individual calibration, and we establish matching upper and lower bounds for the calibration error of our proposed methods. Technically, our analysis combines the nonparametric analysis with a covering number argument for parametric analysis, which advances the existing theoretical analyses in the literature of nonparametric density estimation and quantile bandit problems. Importantly, the nonparametric perspective sheds new theoretical insights into regression calibration in terms of the curse of dimensionality and reconciles the existing results on the impossibility of individual calibration. Numerical experiments show the advantage of such a simple approach under various metrics, and also under covariates shift. We hope our work provides a simple benchmark and a starting point of theoretical ground for future research on regression calibration.

Deep Learning for Choice Modeling

Choice modeling has been a central topic in the study of individual preference or utility across many fields including economics, marketing, operations research, and psychology. While the vast majority of the literature on choice models has been devoted to the analytical properties that lead to managerial and policy-making insights, the existing methods to learn a choice model from empirical data are often either computationally intractable or sample inefficient. In this paper, we develop deep learning-based choice models under two settings of choice modeling: (i) feature-free and (ii) feature-based. Our model captures both the intrinsic utility for each candidate choice and the effect that the assortment has on the choice probability. Synthetic and real data experiments demonstrate the performances of proposed models in terms of the recovery of the existing choice models, sample complexity, assortment effect, architecture design, and model interpretation.