Towards Better Statistical Understanding of Watermarking LLMs

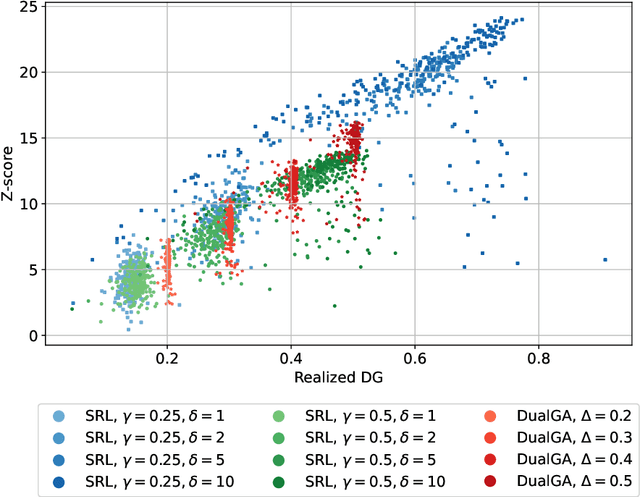
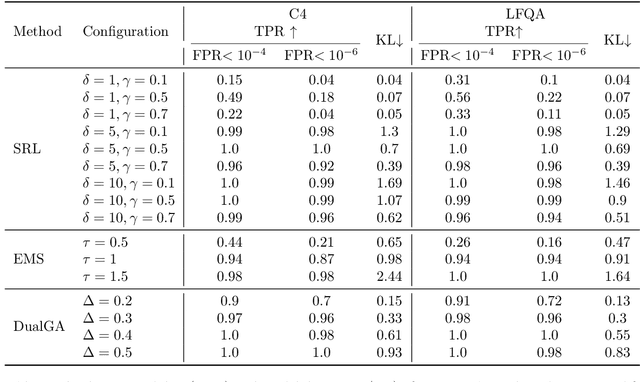
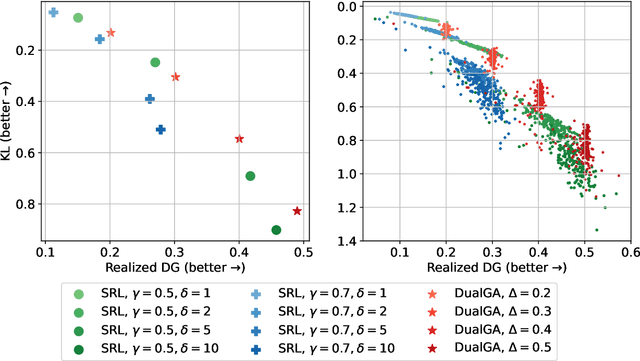
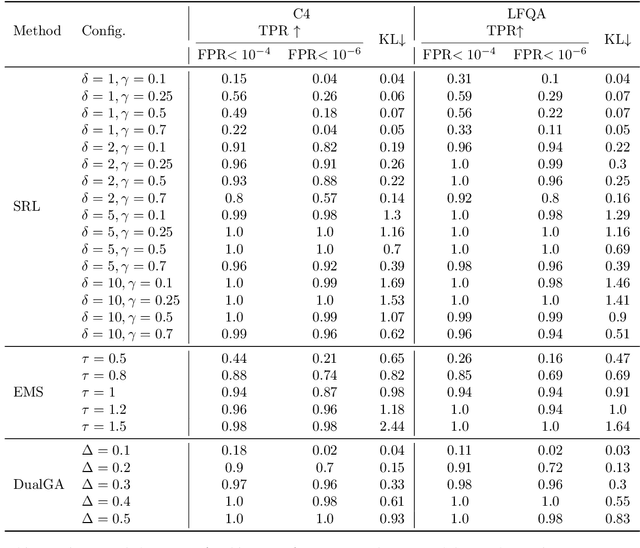
In this paper, we study the problem of watermarking large language models (LLMs). We consider the trade-off between model distortion and detection ability and formulate it as a constrained optimization problem based on the green-red algorithm of Kirchenbauer et al. (2023a). We show that the optimal solution to the optimization problem enjoys a nice analytical property which provides a better understanding and inspires the algorithm design for the watermarking process. We develop an online dual gradient ascent watermarking algorithm in light of this optimization formulation and prove its asymptotic Pareto optimality between model distortion and detection ability. Such a result guarantees an averaged increased green list probability and henceforth detection ability explicitly (in contrast to previous results). Moreover, we provide a systematic discussion on the choice of the model distortion metrics for the watermarking problem. We justify our choice of KL divergence and present issues with the existing criteria of ``distortion-free'' and perplexity. Finally, we empirically evaluate our algorithms on extensive datasets against benchmark algorithms.

Harnessing Diverse Data for Global Disaster Prediction: A Multimodal Framework

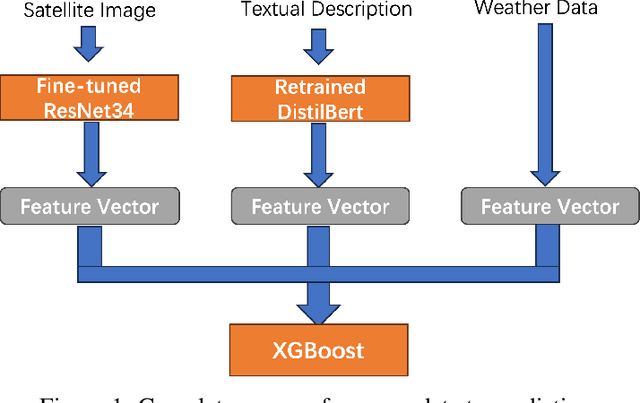
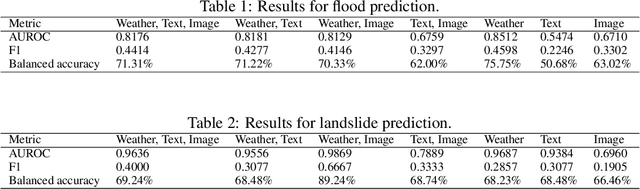
As climate change intensifies, the urgency for accurate global-scale disaster predictions grows. This research presents a novel multimodal disaster prediction framework, combining weather statistics, satellite imagery, and textual insights. We particularly focus on "flood" and "landslide" predictions, given their ties to meteorological and topographical factors. The model is meticulously crafted based on the available data and we also implement strategies to address class imbalance. While our findings suggest that integrating multiple data sources can bolster model performance, the extent of enhancement differs based on the specific nature of each disaster and their unique underlying causes.

Quantile Markov Decision Process

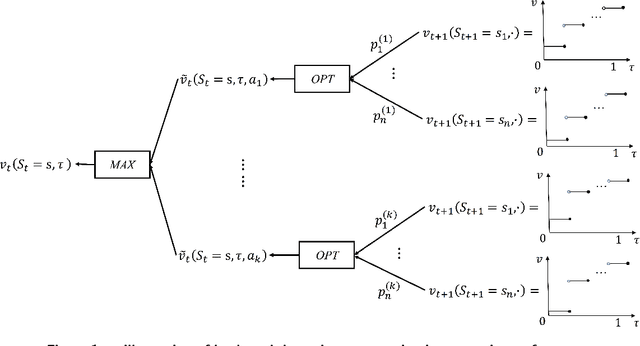
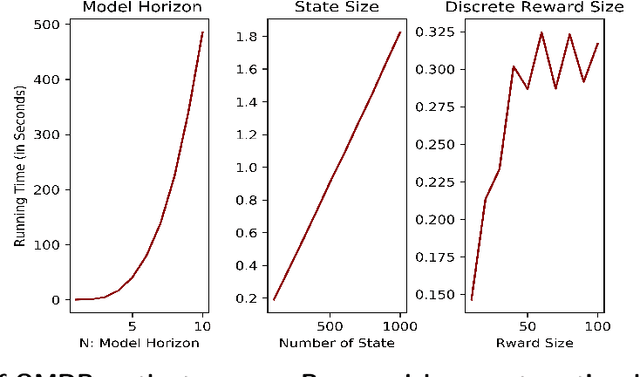
In this paper, we consider the problem of optimizing the quantiles of the cumulative rewards of Markov Decision Processes (MDP), to which we refers as Quantile Markov Decision Processes (QMDP). Traditionally, the goal of a Markov Decision Process (MDP) is to maximize expected cumulative reward over a defined horizon (possibly to be infinite). In many applications, however, a decision maker may be interested in optimizing a specific quantile of the cumulative reward instead of its expectation. Our framework of QMDP provides analytical results characterizing the optimal QMDP solution and presents the algorithm for solving the QMDP. We provide analytical results characterizing the optimal QMDP solution and present the algorithms for solving the QMDP. We illustrate the model with two experiments: a grid game and a HIV optimal treatment experiment.

Hierarchical Modeling of Seed Variety Yields and Decision Making for Future Planting Plans

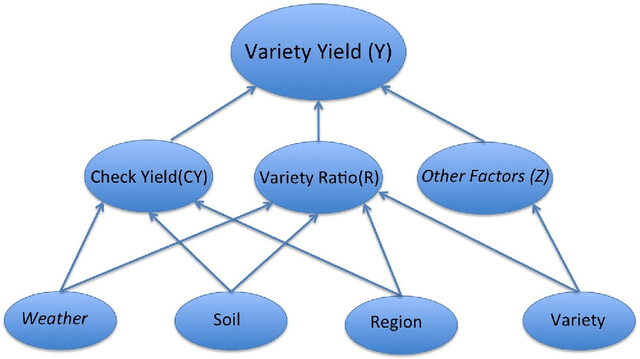
Eradicating hunger and malnutrition is a key development goal of the 21st century. We address the problem of optimally identifying seed varieties to reliably increase crop yield within a risk-sensitive decision-making framework. Specifically, we introduce a novel hierarchical machine learning mechanism for predicting crop yield (the yield of different seed varieties of the same crop). We integrate this prediction mechanism with a weather forecasting model, and propose three different approaches for decision making under uncertainty to select seed varieties for planting so as to balance yield maximization and risk.We apply our model to the problem of soybean variety selection given in the 2016 Syngenta Crop Challenge. Our prediction model achieves a median absolute error of 3.74 bushels per acre and thus provides good estimates for input into the decision models.Our decision models identify the selection of soybean varieties that appropriately balance yield and risk as a function of the farmer's risk aversion level. More generally, our models support farmers in decision making about which seed varieties to plant.