Quantile Markov Decision Process
Paper and Code
Jan 17, 2018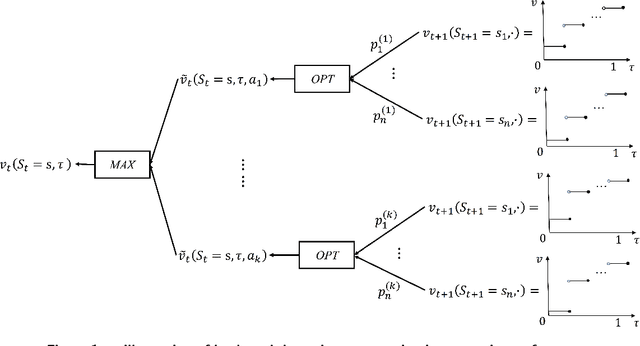


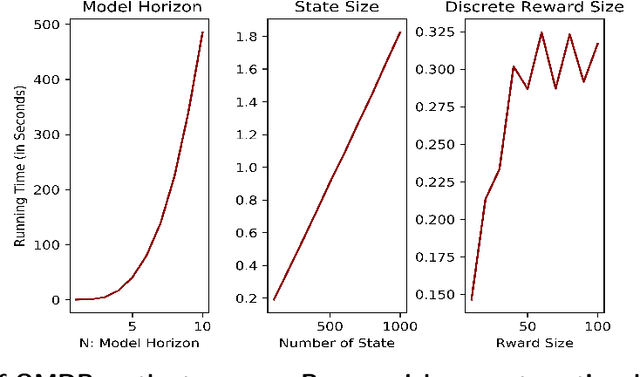
In this paper, we consider the problem of optimizing the quantiles of the cumulative rewards of Markov Decision Processes (MDP), to which we refers as Quantile Markov Decision Processes (QMDP). Traditionally, the goal of a Markov Decision Process (MDP) is to maximize expected cumulative reward over a defined horizon (possibly to be infinite). In many applications, however, a decision maker may be interested in optimizing a specific quantile of the cumulative reward instead of its expectation. Our framework of QMDP provides analytical results characterizing the optimal QMDP solution and presents the algorithm for solving the QMDP. We provide analytical results characterizing the optimal QMDP solution and present the algorithms for solving the QMDP. We illustrate the model with two experiments: a grid game and a HIV optimal treatment experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge