Understanding the Training and Generalization of Pretrained Transformer for Sequential Decision Making

In this paper, we consider the supervised pretrained transformer for a class of sequential decision-making problems. The class of considered problems is a subset of the general formulation of reinforcement learning in that there is no transition probability matrix, and the class of problems covers bandits, dynamic pricing, and newsvendor problems as special cases. Such a structure enables the use of optimal actions/decisions in the pretraining phase, and the usage also provides new insights for the training and generalization of the pretrained transformer. We first note that the training of the transformer model can be viewed as a performative prediction problem, and the existing methods and theories largely ignore or cannot resolve the arisen out-of-distribution issue. We propose a natural solution that includes the transformer-generated action sequences in the training procedure, and it enjoys better properties both numerically and theoretically. The availability of the optimal actions in the considered tasks also allows us to analyze the properties of the pretrained transformer as an algorithm and explains why it may lack exploration and how this can be automatically resolved. Numerically, we categorize the advantages of the pretrained transformer over the structured algorithms such as UCB and Thompson sampling into three cases: (i) it better utilizes the prior knowledge in the pretraining data; (ii) it can elegantly handle the misspecification issue suffered by the structured algorithms; (iii) for short time horizon such as $T\le50$, it behaves more greedy and enjoys much better regret than the structured algorithms which are designed for asymptotic optimality.

Transformer Choice Net: A Transformer Neural Network for Choice Prediction

Discrete-choice models, such as Multinomial Logit, Probit, or Mixed-Logit, are widely used in Marketing, Economics, and Operations Research: given a set of alternatives, the customer is modeled as choosing one of the alternatives to maximize a (latent) utility function. However, extending such models to situations where the customer chooses more than one item (such as in e-commerce shopping) has proven problematic. While one can construct reasonable models of the customer's behavior, estimating such models becomes very challenging because of the combinatorial explosion in the number of possible subsets of items. In this paper we develop a transformer neural network architecture, the Transformer Choice Net, that is suitable for predicting multiple choices. Transformer networks turn out to be especially suitable for this task as they take into account not only the features of the customer and the items but also the context, which in this case could be the assortment as well as the customer's past choices. On a range of benchmark datasets, our architecture shows uniformly superior out-of-sample prediction performance compared to the leading models in the literature, without requiring any custom modeling or tuning for each instance.

A Neural Network Based Choice Model for Assortment Optimization

Discrete-choice models are used in economics, marketing and revenue management to predict customer purchase probabilities, say as a function of prices and other features of the offered assortment. While they have been shown to be expressive, capturing customer heterogeneity and behaviour, they are also hard to estimate, often based on many unobservables like utilities; and moreover, they still fail to capture many salient features of customer behaviour. A natural question then, given their success in other contexts, is if neural networks can eliminate the necessity of carefully building a context-dependent customer behaviour model and hand-coding and tuning the estimation. It is unclear however how one would incorporate assortment effects into such a neural network, and also how one would optimize the assortment with such a black-box generative model of choice probabilities. In this paper we investigate first whether a single neural network architecture can predict purchase probabilities for datasets from various contexts and generated under various models and assumptions. Next, we develop an assortment optimization formulation that is solvable by off-the-shelf integer programming solvers. We compare against a variety of benchmark discrete-choice models on simulated as well as real-world datasets, developing training tricks along the way to make the neural network prediction and subsequent optimization robust and comparable in performance to the alternates.

Deep Learning for Choice Modeling

Choice modeling has been a central topic in the study of individual preference or utility across many fields including economics, marketing, operations research, and psychology. While the vast majority of the literature on choice models has been devoted to the analytical properties that lead to managerial and policy-making insights, the existing methods to learn a choice model from empirical data are often either computationally intractable or sample inefficient. In this paper, we develop deep learning-based choice models under two settings of choice modeling: (i) feature-free and (ii) feature-based. Our model captures both the intrinsic utility for each candidate choice and the effect that the assortment has on the choice probability. Synthetic and real data experiments demonstrate the performances of proposed models in terms of the recovery of the existing choice models, sample complexity, assortment effect, architecture design, and model interpretation.

Learning to Sell a Focal-ancillary Combination

A number of products are sold in the following sequence: First a focal product is shown, and if the customer purchases, one or more ancillary products are displayed for purchase. A prominent example is the sale of an airline ticket, where first the flight is shown, and when chosen, a number of ancillaries such as cabin or hold bag options, seat selection, insurance etc. are presented. The firm has to decide on a sale format -- whether to sell them in sequence unbundled, or together as a bundle -- and how to price the focal and ancillary products, separately or as a bundle. Since the ancillary is considered by the customer only after the purchase of the focal product, the sale strategy chosen by the firm creates an information and learning dependency between the products: for instance, offering only a bundle would preclude learning customers' valuation for the focal and ancillary products individually. In this paper we study learning strategies for such focal and ancillary item combinations under the following scenarios: (a) pure unbundling to all customers, (b) personalized mechanism, where, depending on some observed features of the customers, the two products are presented and priced as a bundle or in sequence, (c) initially unbundling (for all customers), and switch to bundling (if more profitable) permanently once during the horizon. We design pricing and decisions algorithms for all three scenarios, with regret upper bounded by $O(d \sqrt{T} \log T)$, and an optimal switching time for the third scenario.

On Dynamic Pricing with Covariates

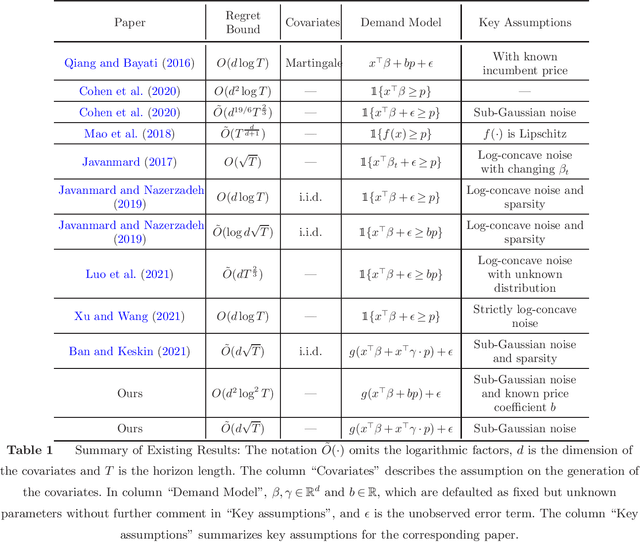
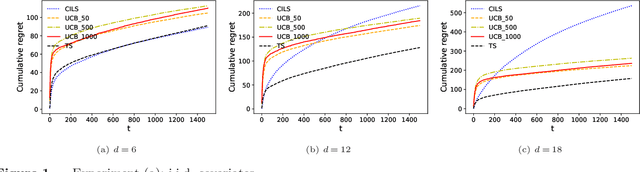
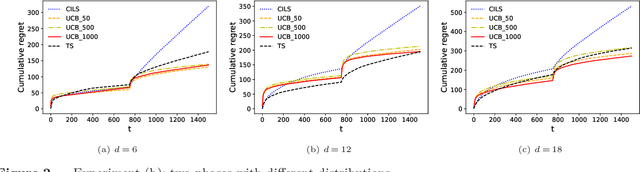
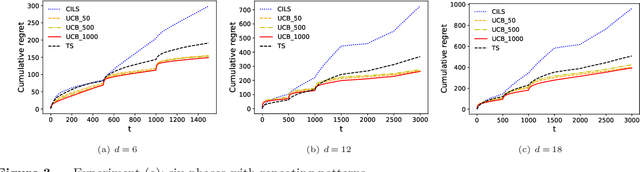
We consider the dynamic pricing problem with covariates under a generalized linear demand model: a seller can dynamically adjust the price of a product over a horizon of $T$ time periods, and at each time period $t$, the demand of the product is jointly determined by the price and an observable covariate vector $x_t\in\mathbb{R}^d$ through an unknown generalized linear model. Most of the existing literature assumes the covariate vectors $x_t$'s are independently and identically distributed (i.i.d.); the few papers that relax this assumption either sacrifice model generality or yield sub-optimal regret bounds. In this paper we show that a simple pricing algorithm has an $O(d\sqrt{T}\log T)$ regret upper bound without assuming any statistical structure on the covariates $x_t$ (which can even be arbitrarily chosen). The upper bound on the regret matches the lower bound (even under the i.i.d. assumption) up to logarithmic factors. Our paper thus shows that (i) the i.i.d. assumption is not necessary for obtaining low regret, and (ii) the regret bound can be independent of the (inverse) minimum eigenvalue of the covariance matrix of the $x_t$'s, a quantity present in previous bounds. Furthermore, we discuss a condition under which a better regret is achievable and how a Thompson sampling algorithm can be applied to give an efficient computation of the prices.