On Dynamic Pricing with Covariates
Paper and Code
Jan 19, 2022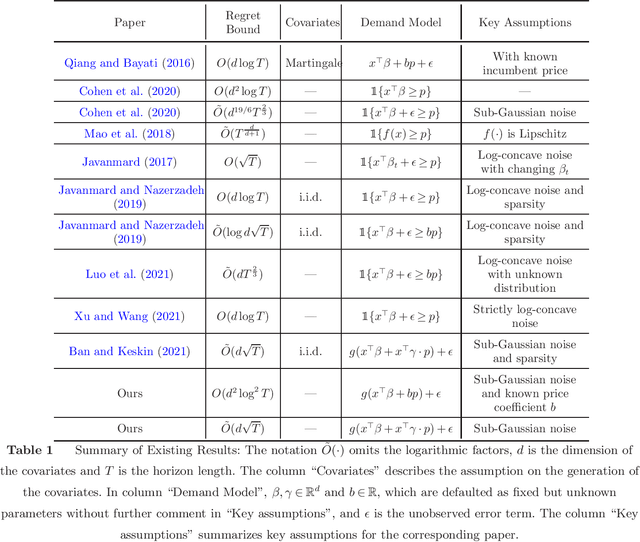
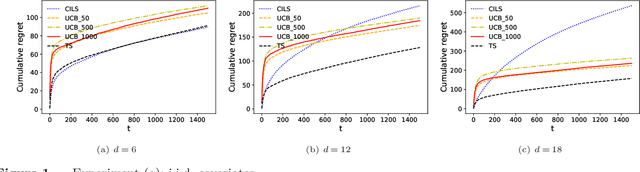
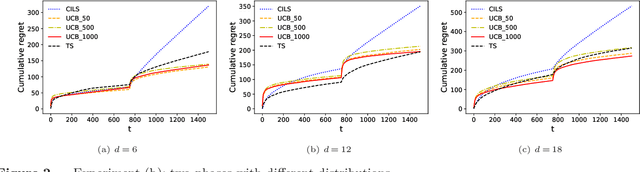
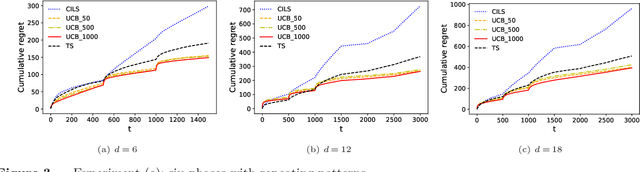
We consider the dynamic pricing problem with covariates under a generalized linear demand model: a seller can dynamically adjust the price of a product over a horizon of $T$ time periods, and at each time period $t$, the demand of the product is jointly determined by the price and an observable covariate vector $x_t\in\mathbb{R}^d$ through an unknown generalized linear model. Most of the existing literature assumes the covariate vectors $x_t$'s are independently and identically distributed (i.i.d.); the few papers that relax this assumption either sacrifice model generality or yield sub-optimal regret bounds. In this paper we show that a simple pricing algorithm has an $O(d\sqrt{T}\log T)$ regret upper bound without assuming any statistical structure on the covariates $x_t$ (which can even be arbitrarily chosen). The upper bound on the regret matches the lower bound (even under the i.i.d. assumption) up to logarithmic factors. Our paper thus shows that (i) the i.i.d. assumption is not necessary for obtaining low regret, and (ii) the regret bound can be independent of the (inverse) minimum eigenvalue of the covariance matrix of the $x_t$'s, a quantity present in previous bounds. Furthermore, we discuss a condition under which a better regret is achievable and how a Thompson sampling algorithm can be applied to give an efficient computation of the prices.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge