Automated Proof of Polynomial Inequalities via Reinforcement Learning

Polynomial inequality proving is fundamental to many mathematical disciplines and finds wide applications in diverse fields. Current traditional algebraic methods are based on searching for a polynomial positive definite representation over a set of basis. However, these methods are limited by truncation degree. To address this issue, this paper proposes an approach based on reinforcement learning to find a {Krivine-basis} representation for proving polynomial inequalities. Specifically, we formulate the inequality proving problem as a linear programming (LP) problem and encode it as a basis selection problem using reinforcement learning (RL), achieving a non-negative {Krivine basis}. Moreover, a fast multivariate polynomial multiplication method based on Fast Fourier Transform (FFT) is employed to enhance the efficiency of action space search. Furthermore, we have implemented a tool called {APPIRL} (Automated Proof of Polynomial Inequalities via Reinforcement Learning). Experimental evaluation on benchmark problems demonstrates the feasibility and effectiveness of our approach. In addition, {APPIRL} has been successfully applied to solve the maximum stable set problem.

A Combinatorial Identities Benchmark for Theorem Proving via Automated Theorem Generation

Large language models (LLMs) have significantly advanced formal theorem proving, yet the scarcity of high-quality training data constrains their capabilities in complex mathematical domains. Combinatorics, a cornerstone of mathematics, provides essential tools for analyzing discrete structures and solving optimization problems. However, its inherent complexity makes it particularly challenging for automated theorem proving (ATP) for combinatorial identities. To address this, we manually construct LeanComb, combinatorial identities benchmark in Lean, which is, to our knowledge, the first formalized theorem proving benchmark built for combinatorial identities. We develop an Automated Theorem Generator for Combinatorial Identities, ATG4CI, which combines candidate tactics suggested by a self-improving large language model with a Reinforcement Learning Tree Search approach for tactic prediction. By utilizing ATG4CI, we generate a LeanComb-Enhanced dataset comprising 260K combinatorial identities theorems, each with a complete formal proof in Lean, and experimental evaluations demonstrate that models trained on this dataset can generate more effective tactics, thereby improving success rates in automated theorem proving for combinatorial identities.

CuDIP: Enhancing Theorem Proving in LLMs via Curriculum Learning-based Direct Preference Optimization

Automated theorem proving (ATP) is one of the most challenging mathematical reasoning tasks for Large Language Models (LLMs). Most existing LLM-based ATP methods rely on supervised fine-tuning, which results in a limited alignment between the theorem proving process and human preferences. Direct Preference Optimization (DPO), which aligns LLMs with human preferences, has shown positive effects for certain tasks. However, the lack of high-quality preference data for theorem proving presents a significant challenge. In this paper, we innovatively apply DPO to formal automated theorem proving and introduces a Curriculum Learning-based DPO Iterative Theorem Proving (CuDIP) method. Specifically, we propose a method for constructing preference data which utilizes LLMs and existing theorem proving data to enhance the diversity of the preference data while reducing the reliance on human preference annotations. We then integrate this preference data construction method with curriculum learning to iteratively fine-tune the theorem proving model through DPO. Experimental results on the MiniF2F and ProofNet datasets demonstrate the effectiveness of the proposed method.

Open-Book Neural Algorithmic Reasoning

Neural algorithmic reasoning is an emerging area of machine learning that focuses on building neural networks capable of solving complex algorithmic tasks. Recent advancements predominantly follow the standard supervised learning paradigm -- feeding an individual problem instance into the network each time and training it to approximate the execution steps of a classical algorithm. We challenge this mode and propose a novel open-book learning framework. In this framework, whether during training or testing, the network can access and utilize all instances in the training dataset when reasoning for a given instance. Empirical evaluation is conducted on the challenging CLRS Algorithmic Reasoning Benchmark, which consists of 30 diverse algorithmic tasks. Our open-book learning framework exhibits a significant enhancement in neural reasoning capabilities. Further, we notice that there is recent literature suggesting that multi-task training on CLRS can improve the reasoning accuracy of certain tasks, implying intrinsic connections between different algorithmic tasks. We delve into this direction via the open-book framework. When the network reasons for a specific task, we enable it to aggregate information from training instances of other tasks in an attention-based manner. We show that this open-book attention mechanism offers insights into the inherent relationships among various tasks in the benchmark and provides a robust tool for interpretable multi-task training.

A Context-Enhanced Framework for Sequential Graph Reasoning

The paper studies sequential reasoning over graph-structured data, which stands as a fundamental task in various trending fields like automated math problem solving and neural graph algorithm learning, attracting a lot of research interest. Simultaneously managing both sequential and graph-structured information in such tasks presents a notable challenge. Over recent years, many neural architectures in the literature have emerged to tackle the issue. In this work, we generalize the existing architectures and propose a context-enhanced framework. The crucial innovation is that the reasoning of each step does not only rely on the outcome of the preceding step but also leverages the aggregation of information from more historical outcomes. The idea stems from our observation that in sequential graph reasoning, each step's outcome has a much stronger inner connection with each other compared to traditional seq-to-seq tasks. We show that the framework can effectively integrate with the existing methods, enhancing their reasoning abilities. Empirical evaluations are conducted on the challenging CLRS Reasoning Benchmark, and the results demonstrate that the proposed framework significantly improves the performance of existing architectures, yielding state-of-the-art results across the majority of the datasets within the benchmark.

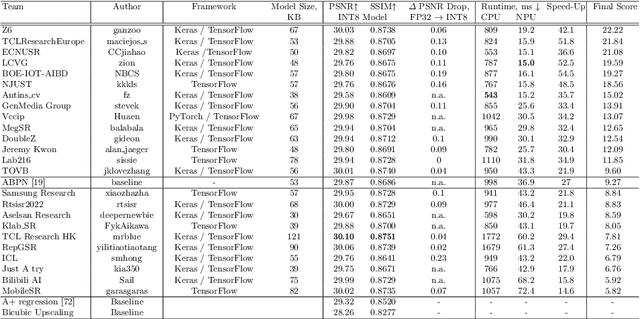
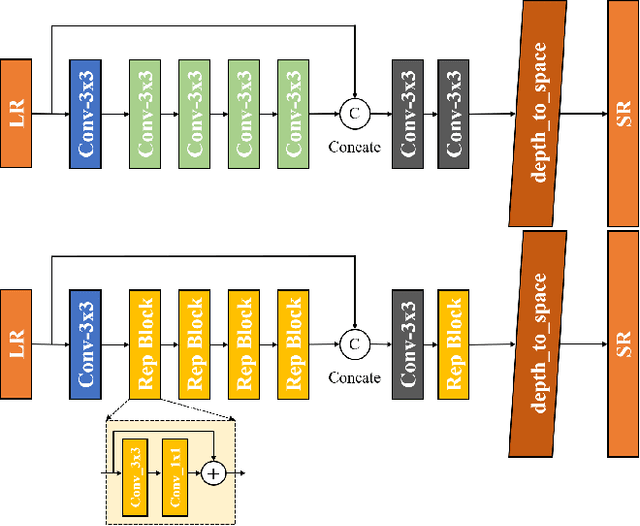
Efficient and Accurate Quantized Image Super-Resolution on Mobile NPUs, Mobile AI & AIM 2022 challenge: Report

Image super-resolution is a common task on mobile and IoT devices, where one often needs to upscale and enhance low-resolution images and video frames. While numerous solutions have been proposed for this problem in the past, they are usually not compatible with low-power mobile NPUs having many computational and memory constraints. In this Mobile AI challenge, we address this problem and propose the participants to design an efficient quantized image super-resolution solution that can demonstrate a real-time performance on mobile NPUs. The participants were provided with the DIV2K dataset and trained INT8 models to do a high-quality 3X image upscaling. The runtime of all models was evaluated on the Synaptics VS680 Smart Home board with a dedicated edge NPU capable of accelerating quantized neural networks. All proposed solutions are fully compatible with the above NPU, demonstrating an up to 60 FPS rate when reconstructing Full HD resolution images. A detailed description of all models developed in the challenge is provided in this paper.