Zheng Cui
PRNet: Original Information Is All You Have
Oct 10, 2025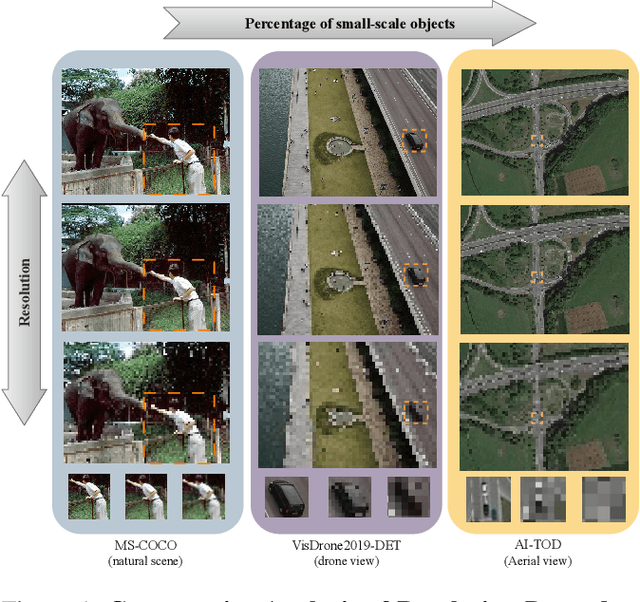
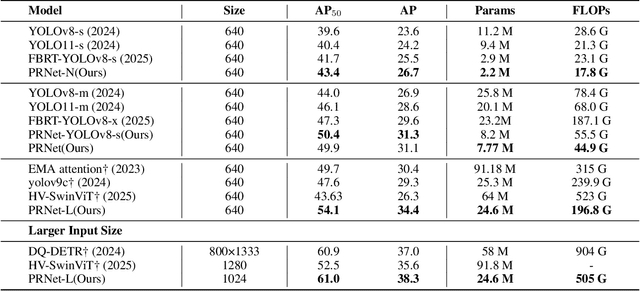
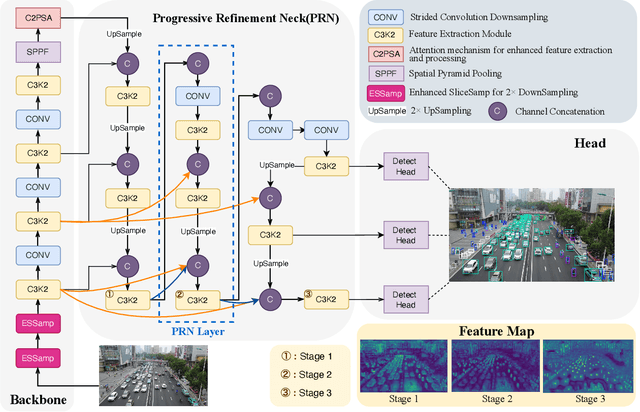
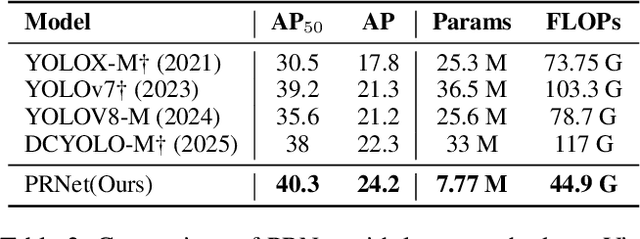
Abstract:Small object detection in aerial images suffers from severe information degradation during feature extraction due to limited pixel representations, where shallow spatial details fail to align effectively with semantic information, leading to frequent misses and false positives. Existing FPN-based methods attempt to mitigate these losses through post-processing enhancements, but the reconstructed details often deviate from the original image information, impeding their fusion with semantic content. To address this limitation, we propose PRNet, a real-time detection framework that prioritizes the preservation and efficient utilization of primitive shallow spatial features to enhance small object representations. PRNet achieves this via two modules:the Progressive Refinement Neck (PRN) for spatial-semantic alignment through backbone reuse and iterative refinement, and the Enhanced SliceSamp (ESSamp) for preserving shallow information during downsampling via optimized rearrangement and convolution. Extensive experiments on the VisDrone, AI-TOD, and UAVDT datasets demonstrate that PRNet outperforms state-of-the-art methods under comparable computational constraints, achieving superior accuracy-efficiency trade-offs.
Fragility-aware Classification for Understanding Risk and Improving Generalization
Feb 18, 2025Abstract:Classification models play a critical role in data-driven decision-making applications such as medical diagnosis, user profiling, recommendation systems, and default detection. Traditional performance metrics, such as accuracy, focus on overall error rates but fail to account for the confidence of incorrect predictions, thereby overlooking the risk of confident misjudgments. This risk is particularly significant in cost-sensitive and safety-critical domains like medical diagnosis and autonomous driving, where overconfident false predictions may cause severe consequences. To address this issue, we introduce the Fragility Index (FI), a novel metric that evaluates classification performance from a risk-averse perspective by explicitly capturing the tail risk of confident misjudgments. To enhance generalizability, we define FI within the robust satisficing (RS) framework, incorporating data uncertainty. We further develop a model training approach that optimizes FI while maintaining tractability for common loss functions. Specifically, we derive exact reformulations for cross-entropy loss, hinge-type loss, and Lipschitz loss, and extend the approach to deep learning models. Through synthetic experiments and real-world medical diagnosis tasks, we demonstrate that FI effectively identifies misjudgment risk and FI-based training improves model robustness and generalizability. Finally, we extend our framework to deep neural network training, further validating its effectiveness in enhancing deep learning models.
IME: Integrating Multi-curvature Shared and Specific Embedding for Temporal Knowledge Graph Completion
Mar 28, 2024



Abstract:Temporal Knowledge Graphs (TKGs) incorporate a temporal dimension, allowing for a precise capture of the evolution of knowledge and reflecting the dynamic nature of the real world. Typically, TKGs contain complex geometric structures, with various geometric structures interwoven. However, existing Temporal Knowledge Graph Completion (TKGC) methods either model TKGs in a single space or neglect the heterogeneity of different curvature spaces, thus constraining their capacity to capture these intricate geometric structures. In this paper, we propose a novel Integrating Multi-curvature shared and specific Embedding (IME) model for TKGC tasks. Concretely, IME models TKGs into multi-curvature spaces, including hyperspherical, hyperbolic, and Euclidean spaces. Subsequently, IME incorporates two key properties, namely space-shared property and space-specific property. The space-shared property facilitates the learning of commonalities across different curvature spaces and alleviates the spatial gap caused by the heterogeneous nature of multi-curvature spaces, while the space-specific property captures characteristic features. Meanwhile, IME proposes an Adjustable Multi-curvature Pooling (AMP) approach to effectively retain important information. Furthermore, IME innovatively designs similarity, difference, and structure loss functions to attain the stated objective. Experimental results clearly demonstrate the superior performance of IME over existing state-of-the-art TKGC models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge