Information Processing Equalities and the Information-Risk Bridge

We introduce two new classes of measures of information for statistical experiments which generalise and subsume $\phi$-divergences, integral probability metrics, $\mathfrak{N}$-distances (MMD), and $(f,\Gamma)$ divergences between two or more distributions. This enables us to derive a simple geometrical relationship between measures of information and the Bayes risk of a statistical decision problem, thus extending the variational $\phi$-divergence representation to multiple distributions in an entirely symmetric manner. The new families of divergence are closed under the action of Markov operators which yields an information processing equality which is a refinement and generalisation of the classical data processing inequality. This equality gives insight into the significance of the choice of the hypothesis class in classical risk minimization.

Generalised Lipschitz Regularisation Equals Distributional Robustness

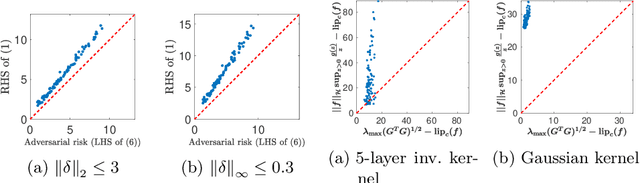
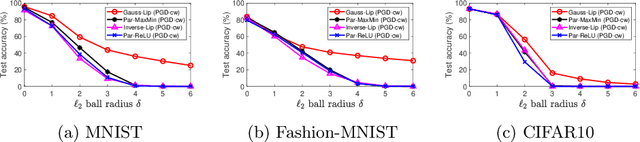
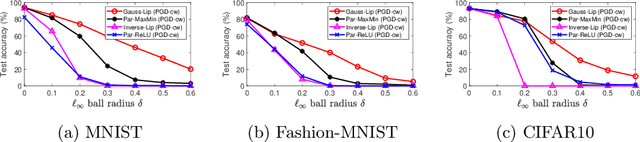
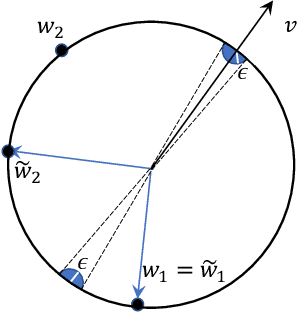
The problem of adversarial examples has highlighted the need for a theory of regularisation that is general enough to apply to exotic function classes, such as universal approximators. In response, we give a very general equality result regarding the relationship between distributional robustness and regularisation, as defined with a transportation cost uncertainty set. The theory allows us to (tightly) certify the robustness properties of a Lipschitz-regularised model with very mild assumptions. As a theoretical application we show a new result explicating the connection between adversarial learning and distributional robustness. We then give new results for how to achieve Lipschitz regularisation of kernel classifiers, which are demonstrated experimentally.

Proper-Composite Loss Functions in Arbitrary Dimensions

The study of a machine learning problem is in many ways is difficult to separate from the study of the loss function being used. One avenue of inquiry has been to look at these loss functions in terms of their properties as scoring rules via the proper-composite representation, in which predictions are mapped to probability distributions which are then scored via a scoring rule. However, recent research so far has primarily been concerned with analysing the (typically) finite-dimensional conditional risk problem on the output space, leaving aside the larger total risk minimisation. We generalise a number of these results to an infinite dimensional setting and in doing so we are able to exploit the familial resemblance of density and conditional density estimation to provide a simple characterisation of the canonical link.

Monge beats Bayes: Hardness Results for Adversarial Training

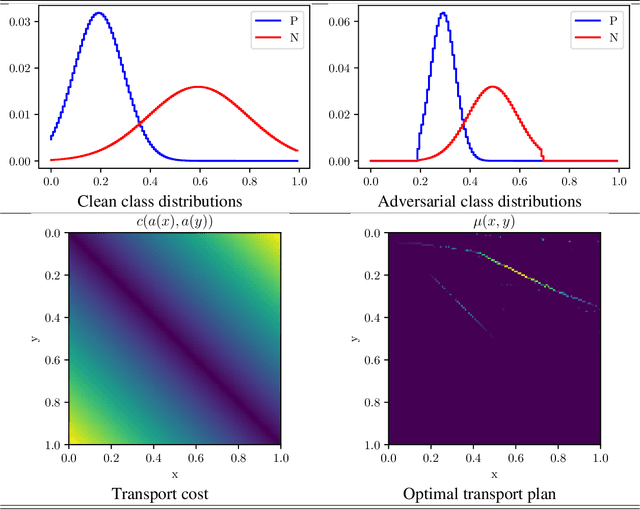
The last few years have seen extensive empirical study of the robustness of neural networks, with a concerning conclusion: several state-of-the-art approaches are highly sensitive to adversarial perturbations of their inputs. There has been an accompanying surge of interest in learning including defense mechanisms against specific adversaries, known as adversarial training. Despite some impressive advances, little remains known on how to best frame a resource-bounded adversary so that it can be severely detrimental to learning, a non-trivial problem which entails at a minimum the choice of loss and classifiers. We suggest here a formal answer to this question, and pin down a simple sufficient property for any given class of adversaries to be detrimental to learning. This property involves a central measure of `harmfulness' which generalizes the well-known class of integral probability metrics. A key feature of our result is that it holds for \textit{all} proper losses, and for a popular subset of these, the optimisation of this central measure appears to be independent of the loss. We show how weakly contractive adversaries for a RKHS can be self-combined to build a maximally detrimental adversary, we show that some implemented existing adversaries involve proxies of our optimal transport adversaries and finally provide a toy experiment assessing such adversaries in a simple context, displaying that additional robustness on testing can be granted through adversarial training.

Integral Privacy for Sampling from Mollifier Densities with Approximation Guarantees

Sampling encompasses old and central problems in statistics and machine learning. There exists several approaches to cast this problem in a differential privacy framework but little is still comparatively known about the approximation guarantees of the unknown density by the private one learned. In this paper, we first introduce a general condition for a set of densities, called an $\varepsilon$-mollifier, to grant privacy for sampling in the $\varepsilon$-differential privacy model, and even in a stronger model where we remove the famed adjacency condition of inputs. We then show how to exploit the boosting toolkit to learn a density within an $\varepsilon$-mollifier with guaranteed approximation of the target density that degrade gracefully with the privacy budget. Approximation guarantees cover the mode capture problem, a problem which is receiving a lot of attention in the generative models literature. To our knowledge, the way we exploit the boosting toolkit has never been done before in the context of density estimation or sampling: we require access to a weak learner in the original boosting sense, so we learn a density out of \textit{classifiers}. Experimental results against a state of the art implementation of private kernel density estimation display that our technique consistently obtains improved results, managing in particular to get similar outputs for a privacy budget $\epsilon$ which is however orders of magnitude smaller.

Lipschitz Networks and Distributional Robustness

Robust risk minimisation has several advantages: it has been studied with regards to improving the generalisation properties of models and robustness to adversarial perturbation. We bound the distributionally robust risk for a model class rich enough to include deep neural networks by a regularised empirical risk involving the Lipschitz constant of the model. This allows us to interpretand quantify the robustness properties of a deep neural network. As an application we show the distributionally robust risk upperbounds the adversarial training risk.

Boosted Density Estimation Remastered

There has recently been a steady increase in the number iterative approaches to density estimation. However, an accompanying burst of formal convergence guarantees has not followed; all results pay the price of heavy assumptions which are often unrealistic or hard to check. The Generative Adversarial Network (GAN) literature --- seemingly orthogonal to the aforementioned pursuit --- has had the side effect of a renewed interest in variational divergence minimisation (notably $f$-GAN). We show that by introducing a weak learning assumption (in the sense of the classical boosting framework) we are able to import some recent results from the GAN literature to develop an iterative boosted density estimation algorithm, including formal convergence results with rates, that does not suffer the shortcomings other approaches. We show that the density fit is an exponential family, and as part of our analysis obtain an improved variational characterisation of $f$-GAN.

f-GANs in an Information Geometric Nutshell

Nowozin \textit{et al} showed last year how to extend the GAN \textit{principle} to all $f$-divergences. The approach is elegant but falls short of a full description of the supervised game, and says little about the key player, the generator: for example, what does the generator actually converge to if solving the GAN game means convergence in some space of parameters? How does that provide hints on the generator's design and compare to the flourishing but almost exclusively experimental literature on the subject? In this paper, we unveil a broad class of distributions for which such convergence happens --- namely, deformed exponential families, a wide superset of exponential families --- and show tight connections with the three other key GAN parameters: loss, game and architecture. In particular, we show that current deep architectures are able to factorize a very large number of such densities using an especially compact design, hence displaying the power of deep architectures and their concinnity in the $f$-GAN game. This result holds given a sufficient condition on \textit{activation functions} --- which turns out to be satisfied by popular choices. The key to our results is a variational generalization of an old theorem that relates the KL divergence between regular exponential families and divergences between their natural parameters. We complete this picture with additional results and experimental insights on how these results may be used to ground further improvements of GAN architectures, via (i) a principled design of the activation functions in the generator and (ii) an explicit integration of proper composite losses' link function in the discriminator.